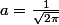Sulaheia a écrit:Merci à tous les deux pour vos réponses.
Lostounet, je ne comprends pas tout ce que tu dis, même avec google pour m'expliquer un peu, mais j'aime bien savoir qu'il y a d'autres choses après - ça me motive pour découvrir la suite.
En fait j'ai fait des maths après le bac, donc je devrais savoir tout ça - peut être que j'aurais dû aller en cours de temps en temps

.
Je vais essayer de détailler un peu. Voici une méthode "élémentaire" qui permet de trouver rapidement la valeur de a (relativement aux autres méthodes...)
Par exemple, si X suit la loi normale N(0 ; 1), nous savons qu'elle possède une densité sur R (non sur un segment comme pour tout exercice) de la forme:
 = a exp(-\frac{x^2}{2}))
avec a une certaine constante à trouver.
Donc en utilisant la méthode que tu as dit, c'est à dire qu'on cherche à trouver la valeur de a en calculant l'intégrale de p(x) sur le domaine (donc ici R), on veut donc calculer:
dx} = 1 \\ \int_{-\infty}^{+\infty}{a exp(\frac{-x^2}{2})dx} = 1)
On doit donc choisir a pour que ce soit effectivement une densité:
dx} = 1)
Malheureusement, on est ici bloqué vu que la fonction exp(-x^2)/2 n'a pas de primitive (avec les fonctions usuelles). Donc on va quand même essayer de calculer de calculer l'intégrale sans primitiver directement.
Notons alors I l'intégrale:
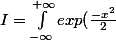dx})
Vu que la variable d'intégration est muette, on pourrait aussi dire
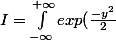dy})
Maintenant l'astuce consiste à multiplier membre à membre ces deux équations:
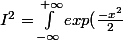dx} \times \int_{-\infty}^{+\infty}{exp(\frac{-y^2}{2})dy})
Maintenant il existe un théorème (de Fubini-Tonelli), qui nous dit que si les deux intégrales sont "indépendantes" on peut regrouper de la manière suivante:
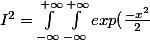} \times exp(\frac{-y^2}{2}) dx dy}<br />= \int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty} exp(- \frac{x^2 + y^2}{2})dx dy)
C'est ici qu'on va opérer: x^2 + y^2 rappelle l'équation d'un cercle ! Quand x et y décrivent R, les x^2 + y^2 "sont des cercles" de rayon disons r et on peut dire que
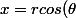 \\ y = r sin(\theta))
pour

. Donc plutot que x et y décrivent R et R, on peut essayer de faire décrire r et theta, R+ et [0 ; 2pi], c'est exactement le même domaine d'intégration. Cela s'appelle changement de variable polaire.
Ce qui signifie (on pourra revenir sur les deux lignes en détail si jamais)
/2 = r^2/2)
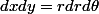
Et que r décrit R+ et theta décrit [0 ; 2pi]
Ce qui implique:
dr d\theta)
Rebelote avec le théorème qui permet de séparer les intégrales ! Mais dans l'autre sens:
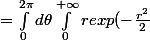dr)
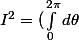 \times (\int_{0}^{+\infty} (r exp(- \frac{r^2}{2}))dr)
Et cette fois-ci nous disposons d'une primitive pour l'intégrale à droite grâce au r qui est apparu dans le changement de variable
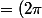 \times [-exp(-x^2/2)]_0^{\infty} =( 2 \pi) \times (1))
Donc:
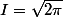
Alors
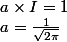
Ainsi pour que p(x) soit une densité il faut choisir