Bonsoir j'aurai besoin de votre aide s'il vous plait
On lance deux dés cubiques parfaits portant les numéros de 1 à 6. A chaque lancer on associe la somme S des numéros obtenus.Quelle est la loi de probabilité de la variable aléatoire S
Je n'ai pas compris le principe de cette loi
Loi d'une variable aléatoire
5 messages
- Page 1 sur 1
Salut !
A chaque lancers, on peut associer un couple d'entiers) tels que
tels que  est le numéro obtenu avec le premier dé et
est le numéro obtenu avec le premier dé et  le numéro obtenu avec le second dé.
le numéro obtenu avec le second dé.
Ainsi, exprime, par définition de donnée dans l'énoncé,
donnée dans l'énoncé,  en fonction de
en fonction de  et
et  .
.
Soit l'ensemble de tous les couples
l'ensemble de tous les couples ) ; quel est le cardinal
; quel est le cardinal ) de
de  ?
?
Soit) l'ensemble des valeurs possibles que peut prendre
l'ensemble des valeurs possibles que peut prendre  pour
pour \in \Omega) . Explicite les éléments de
. Explicite les éléments de ) .
.
Dans cet exercice, on travaille avec des dés supposés cubique parfait donc il n'y a aucune raison de tomber plus sur un chiffre que sur un autre. En conséquence, on utilisera la probabilité dite uniforme.
Pour un élément) , trouver la loi de
, trouver la loi de  revient à calculer la probabilité de que
revient à calculer la probabilité de que 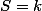 i.e. calculer pour
i.e. calculer pour ) ,
, 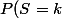=<br />\frac{\rm nombre\ de\ cas\ favorables}{\rm nombre\ de\ cas\ possibles}= \frac{ {\rm card}\left( \left{ (x,y) \mid S=k \right} \right) }{ {\rm card} (\Omega ) }) .
.
Proriko a écrit:Bonsoir j'aurai besoin de votre aide s'il vous plait
On lance deux dés cubiques parfaits portant les numéros de 1 à 6. A chaque lancer on associe la somme S des numéros obtenus.Quelle est la loi de probabilité de la variable aléatoire S
Je n'ai pas compris le principe de cette loi
A chaque lancers, on peut associer un couple d'entiers
Ainsi, exprime, par définition de
Soit
Soit
Dans cet exercice, on travaille avec des dés supposés cubique parfait donc il n'y a aucune raison de tomber plus sur un chiffre que sur un autre. En conséquence, on utilisera la probabilité dite uniforme.
Pour un élément
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Proriko a écrit:Vous êtes sur que je dois exprimer tout cela? Je ne suis qu'en 1ère S :p
Je ne suis pas cencé faire l'espace de schéma avec les branches , et réalisé un tableau en utilisant quelque chose du genre X=x1 ?
Comme la plupart des exercices, la manière de le résoudre n'est pas unique.
Si tu as compris ce que cela signifie qu'une variable aléatoire suit une loi uniforme, alors tu peux toujours représenter dans un tableau lensemble des couples (x,y) et voir pour combien de cases on a S=k. La probabilité sera alors le nombre de cases sur l'univers dans lequel con considère l'expérience :+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Pour tout vous dire je n'ai vraiment rien compris.
Si j'ai dis ça c'est que je l'ai vu dans "l'aide" juste au dessus de l'exercice mais c'est très vague pour moi...
J'aimerais bien finir cette exercice mais je n'y arrive pas du tout , surtout que je suis fatigué et qu'il est pour demain à la premiere heure...
Si j'ai dis ça c'est que je l'ai vu dans "l'aide" juste au dessus de l'exercice mais c'est très vague pour moi...
J'aimerais bien finir cette exercice mais je n'y arrive pas du tout , surtout que je suis fatigué et qu'il est pour demain à la premiere heure...
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
