Kikoo <3 Bieber a écrit:La loi uniforme est une loi probabiliste qui donne à chaque réel de ce segment une probabilité d'être tiré au sort. Comme il s'agit d'une loi uniforme, chaque réel a la même chance d'être tiré.
C'est pas terrible de présenter la situation comme ça, car en réalité, chaque réel a une probabilité nulle d'être tiré.
Kikoo <3 Bieber a écrit:Et comme on travaille dans du continu, on désigne par une certaine fonction f la proba sur [a,b] de tirer un certain nombre. On l'appelle la densité de probabilité de la loi uniforme associée à ce tirage, et elle a une valeur constante sur [a,b].
La densité de probabilité f n'est pas vraiment la proba de tirer un nombre (car cette dernière est nulle). Il faut bien assimiler la définition d'une densité de proba, ici uniforme : c'est
 = \int_i^j f(t) dt)
pour tous

.
D'ailleurs, on voit bien que
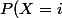 = 0)
en posant j=i.
Kikoo <3 Bieber a écrit:On cherche donc à savoir ce que vaut cette fonction constante, constante que l'on nomme l. Or on sait que si l'on somme toutes les probas sur l'ensemble [a,b], on obtiendra 1, logique.
Nous résolvons donc l'équation l*(b-a)=1 (visuellement, l'aire du rectangle de hauteur f(x)=l entre a et b, x appartenant à [a,b]).
Nous trouvons que l=1/(b-a), qui est donc la densité de probabilité de notre loi.
Effectivement, on trouve ainsi f(t) = 1/(b-a).
Kikoo <3 Bieber a écrit:PS : pour la question, il doit donc y avoir un hic !
Je suis d'accord.
Linette-55, il y a un binz dans ce que tu as pris en note car c'est
 = \int_x^{x+dx} f(t) dt = \int_x^{x+dx} 1/(b-a) dt = (x+dx-x)/(b-a) = dx/(b-a))
