Loi normale

[ben124]

Bonsoir,

j'ai une question relative à l’échantillonnage dans les tests statistiques: existe t-il une formule mathématique reliant l'écart-type à l'échantillon d'un test statistique? Pour pouvoir déterminer quel écart-type il me faut lorsque j'utilise un faible échantillon, et inversement lorsque j'en utilise un plus grand.

Petite précision: je ne sais pas si je ne suis pas en train de dire une grosse connerie en disant que l'écart-type peut varier pour une même moyenne. Si l'écart-type est une donnée fixe, alors ma question serait: de combien faut t-il faire varier l'écart-type selon la taille de l'échantillon (pour avoir un test significatif)?

[Anonyme]

@ben124

Est ce que tu comprends les explications ci dessous :

Si , sur une population donnée , le pourcentage (ou la fréquence) d'un caractère donné est de f
alors sur un échantillon de taille n (tiré "au hasard" dans la population)
l'intervalle de fluctuation au seuil de 95% est 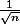: [ f - , f + ]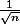

Si c'est le cas , peux tu répondre aux 2 questions suivantes :
1) Qu'est ce qu'un échantillon de taille n dans une population donnée ?

2) Quelle est la loi de probabilité que suit le nombre d'individus qui ont "un caractère donné" dans un échantillon de taille n ?

ps)
Ces notions sont enseignées en classe de seconde et sont approfondies en classe de 1ere et de terminale

[ben124]

@ben124

Est ce que tu comprends les explications ci dessous :

Si , sur une population donnée , le pourcentage (ou la fréquence) d'un caractère donné est de f
alors sur un échantillon de taille n (tiré "au hasard" dans la population)
l'intervalle de fluctuation au seuil de 95% est : [ f - , f + ]

Si c'est le cas , peux tu répondre aux 2 questions suivantes :
1) Qu'est ce qu'un échantillon de taille n dans une population donnée ?

2) Quelle est la loi de probabilité que suit le nombre d'individus qui ont "un caractère donné" dans un échantillon de taille n ?

ps)
Ces notions sont enseignées en classe de seconde et sont approfondies en classe de 1ere et de terminale

1) échantillon= "groupe" représentatif de la population étudiée

2) alors là je sais pas du tout

Merci en tout cas de ta réponse!

Donc dans ta formule, on peut approximer 1/racine (n) à l'écart-type?

[Anonyme]

1) échantillon= "groupe" représentatif de la population étudiée

Pas exactement....

Voici quelques rappels du cours ( avant d'évoquer une loi normale de moyenne et d'écart type )

Il faut d'abord savoir ou comprendre :

1) ce qu'est un échantillon de taille dans une population donnée :

un échantillon de taille n est analogue à un tirage de boules avec remise dans une urne qui contient un nombre de boule ) (*)

2) Ensuite il faut comprendre ce qu'est une loi de Bernouilli de paramètre ,
( c'était la réponse qu'il fallait donner à la 2eme question de mon message précédent )

3) Puis via le théorème "Central Limit" , on peut sous certaines conditions faire une approximation de cette loi binomiale par une loi normale...

Est ce que tu as compris quelque chose ?

Si oui : peux tu donner l'approximation qu'on peut faire ?

Si non : essaie de lire ton cours de maths sur ces notions et tu comprendras ce que j'essaie de t'expliquer

Et pour répondre à ta question : plus la taille de l'échantillon est grande (plus n est grand) , plus l'intervalle de fluctuation est petit
mais pas le risque d'erreur reste toujours au seuil de 95%
( le risque d'erreur est le risque d'observer un échantillon dit "EXCEPTIONNEL" ou "NON NORMALE")

De plus sur une population dont on cherche à estimer un écart type à partir de l'observation d'un échantillon de taille n :
une estimation dite ponctuelle (dite non biaisée) de cet écart type est


ps1)
(*)
Si la taille de la population est "conséquente"
alors comme dans un échantillon de taille n , la probabilité de tirer 2 fois le même individu est très faible ,
on peut faire "une approximation" en considérant un échantillon de taille n comme un tirage de n boules SANS remise

ps2)
D'après ce que j'ai lu sur Maths-Forum, ce forum est devenu une véritable BIBLE sur la loi Normale.
Il y a pleins de très longues discussions sur le sujet : La loi normale & Les mesures

Je te déconseille de les lire car à la fin tu ne sais même plus comment tu t'appelles !

A+

[ben124]

Lol tu me fais un vrai cours de math là lol!!

Merci beaucoup en tout cas ça m'est vraiment utile!
Pour répondre à ta question: en fait je sais pas trop mes cours de math sont assez loin... Je post dans la section lycée mais je suis en fac de médecine donc les cours de math yen a pas trop... Mais je vais quand même tenter une réponse: approximation par une loi normale centrée réduite? (un peu au pif j'avoue...)

[Anonyme]

un peu au pif j'avoue...

Je sais que les proba c'est assez intuitif...

mais en général le pif et les maths : il vaut mieux éviter à moins de s'appeler Albert Einstein....

[Anonyme]

Je post dans la section lycée mais je suis en fac de médecine donc les cours de math yen a pas trop...

Procure toi (dans ta blibli universitaire) un livre de maths niveau classe de Terminale ( attention le bouquin doit traiter le nouveau programme qui est en place c'est à dire : 2012-2013 ) et tu auras 3 chapitres sur ces sujets sur les échantillonnages ( qui en médecine sont des sujets importants )

[Anonyme]

Pas exactement....
Voici quelques rappels du cours

3) Puis via le théorème "Central Limit" , on peut sous certaines conditions faire une approximation de cette loi binomiale par une loi normale...

@ben124
Je t'ai raconté une grosse connerie : ce ne n'est pas le théorème central limit (TCL) mais le Théorème de Moivre Laplace

Désolé pour cette boulette

Pour me faire pardonner : clique sur le lien ci dessous et tu auras encore plus d'info
http://www.viewdocsonline.com/document/9p8fjp

[ben124]

@ben124
Je t'ai raconté une grosse connerie : ce ne n'est pas le théorème central limit (TCL) mais le Théorème de Moivre Laplace

Désolé pour cette boulette

Pour me faire pardonner : clique sur le lien ci dessous et tu auras encore plus d'info
http://www.viewdocsonline.com/document/9p8fjp

Ok merci beaucoup pour toutes ces infos!

[Anonyme]

Bonjour à toutes et à tous

Est ce qu'un'e) internaute de Maths-Forum pourrait valider ou corriger mon message en date du 2 novembre dans cette discussion.

ou de m'expliquer à partir de la notion d'échantillonnage : la notion d'estimation ponctuelle d'un écart type.

Merci d'avance.

Référence de mon message : http://www.maths-forum.com/showthread.php?p=881933#post881933

Ma GRANDE interrogation sur ce sujet est :
je pense avoir compris et savoir estimer une moyenne d'une population donnée à partir de l'analyse d'un échantillon de taille n
(avec la notion d'intervalle de confiance à un taux de 95% par exemple)

par contre je ne sais pas comment estimer à partir de cet échantillon un écart type
et surtout je ne sais pas trop à quoi cela sert ?

[Anonyme]

BMa GRANDE interrogation est :
je pense avoir compris et savoir estimer une moyenne d'une population donnée à partir de l'analyse d'un échantillon de taille n
(avec la notion d'intervalle de confiance à un taux de 95% par exemple)

par contre je ne sais pas comment estimer à partir de cet échantillon un écart type
et surtout je ne sais pas trop à quoi cela sert ?

un petit UP
Merci pour vos éventuelles indications d'articles à lire (ou de cours à étudier)

[Joker62]

Bonsoir,

Je ne comprend ce que tu entends par : estimer une moyenne d'une population dans un échantillon.

Généralement, un échantillon de taille n, c'est la donnée de n résultats d'une même expérience aléatoire répétée de façon indépendante. (Ou le tirage de bille dans une urne avec remise oeuf course !)

Si on s'intéresse à un caractère X de la population initiale, alors on peut avoir une estimation de la fréquence de ce caractère dans mon échantillon.
On parle d'intervalle de fluctuation.

Si je ne connais pas la population initiale mais que j'ai un échantillon. Alors là on peut estimer la proportion du caractère X dans la population initiale grâce à la fréquence de ce caractère dans mon échantillon (à hauteur de 95% bien sûr). On parle d'intervalle de confiance et c'est ce qu'on utilise comme test qualité en fin de chaine automobile par exemple.

En gros tu cherches un équivalent de l'intervalle de confiance pour la variance ?

[Anonyme]

@Joker62

La réponse à ta question est OUI

Voici quelques explications supplémentaires :
On ne connait rien sur la population globale

A partir d'un échantillon de taille n , on peut faire une estimation "dite ponctuelle" d'une moyenne ou d'une proportion d'un caractère donné (avec une certaine fiabilité)

Peut on faire la même chose pour estimer le vrai écart type de la population globale à partir d'un échantillonnage ?

Et si oui à quoi cela sert-il ?