Loi binomiale - Compréhension simple
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
upium666
- Membre Relatif
- Messages: 404
- Enregistré le: 14 Mai 2012, 21:44
-
 par upium666 » 23 Avr 2013, 11:19
par upium666 » 23 Avr 2013, 11:19
Bonjour à tous et à toutes
Soit

une variable aléatoire telle que
)
\in\mathbb{N}^2)
Pourquoi
=P(X\leq b)-P(X\leq a))
?
Merci de me l'expliquer :happy2:

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 23 Avr 2013, 11:59
par leon1789 » 23 Avr 2013, 11:59
Salut,
pour toi, que représente
)
,
)
,
)
?
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 23 Avr 2013, 11:59
par Sylviel » 23 Avr 2013, 11:59
En fait c'est vrai quelle que soit la loi de X.
Soit X une variable aléatoire.
 = P (X \in ]- \infty, a] \cup ]a;b]))
or les deux segments sont disjoint donc
 = P (X \in ]- \infty, a]) + P(X\in]a;b]))
Ce qui se réécrit plus simplement
 = P (X \leq a) + P(a< X \leq b))
ce qui va te donner ton égalité.
Une manière plus intuitive de comprendre :
X est entre a et b si il est en dessous de b mais pas en dessous de a.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 23 Avr 2013, 12:15
par Kikoo <3 Bieber » 23 Avr 2013, 12:15
upium666 a écrit:Bonjour à tous et à toutes
Soit

une variable aléatoire telle que
)
\in\mathbb{N}^2)
Pourquoi
=P(X\leq b)-P(X\leq a))
?
Merci de me l'expliquer :happy2:
Salut,
 = \sum_{k=0}^{a}{n \choose k} \, p^k (1-p)^{n-k})
,
 = \sum_{k=0}^{b}{n \choose k} \, p^k (1-p)^{n-k})
. Si b>a, alors
-P(X\leq a)=\sum_{k=0}^{b}{n \choose k} \, p^k (1-p)^{n-k}-\sum_{k=0}^{a}{n \choose k} \, p^k (1-p)^{n-k}=\sum_{k=a+1}^{b}{n \choose k} \, p^k (1-p)^{n-k}=P(a\leq X\leq b))
(Désolé je ne vous ai pas vu vous deux ! Mais ce que j'ai écrit est-il juste ?)
Edit : On écrira plutôt
)
.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 23 Avr 2013, 12:42
par leon1789 » 23 Avr 2013, 12:42
oui, c'est correct, sauf sur un point précis. Mais c'est l'énoncé qui est défectueux.
Regarde, Sylviel a bien fait attention à inclure/exclure la valeur

avec l'emploi des symboles

ou
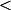

-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 23 Avr 2013, 15:18
par Kikoo <3 Bieber » 23 Avr 2013, 15:18
leon1789 a écrit:oui, c'est correct, sauf sur un point précis. Mais c'est l'énoncé qui est défectueux.
Regarde, Sylviel a bien fait attention à inclure/exclure la valeur

avec l'emploi des symboles

ou
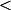

Effectivement, je me disais aussi que ça sonnait faux ! :id:
-
upium666
- Membre Relatif
- Messages: 404
- Enregistré le: 14 Mai 2012, 21:44
-
 par upium666 » 24 Avr 2013, 15:23
par upium666 » 24 Avr 2013, 15:23
Bonjour à tous !
Donc c'est plutôt
=P(X\leq b)-P(X\leq a-1))
?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 24 Avr 2013, 16:26
par leon1789 » 24 Avr 2013, 16:26
oui :lol3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 89 invités