Logique
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
bouyanna
- Membre Naturel
- Messages: 11
- Enregistré le: 26 Jan 2010, 01:06
-
 par bouyanna » 19 Aoû 2014, 16:43
par bouyanna » 19 Aoû 2014, 16:43
Salut tout le monde je cherche une methode pour montrer pour les naturels si 3n+1 est un caré alors n+1 est la somme de trois carés.
Merci d'avance.
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 19 Aoû 2014, 17:34
par Shew » 19 Aoû 2014, 17:34
bouyanna a écrit:Salut tout le monde je cherche une methode pour montrer pour les naturels si 3n+1 est un caré alors n+1 est la somme de trois carés.
Merci d'avance.
Donc
^2 = 3n + 1)
-
bouyanna
- Membre Naturel
- Messages: 11
- Enregistré le: 26 Jan 2010, 01:06
-
 par bouyanna » 19 Aoû 2014, 17:48
par bouyanna » 19 Aoû 2014, 17:48
Merci pour votre reponse.
Le probléme que 3n+1 n'est pas un caré pour tous les n naturels sauf dans certaines comme 3*40+1=121=11^2 où n=40 et n+1=41=1+4+36=1^2+2^2+6^2.
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 19 Aoû 2014, 17:53
par Shew » 19 Aoû 2014, 17:53
bouyanna a écrit:Merci pour votre reponse.
Le probléme que 3n+1 n'est pas un caré pour tous les n naturels sauf dans certaines comme 3*40+1=121=11^2 où n=40 et n+1=41=1+4+36=1^2+2^2+6^2.
Le but est il de chercher trois nombres ayant pour sommes n + 1, ou de montrer que la somme de trois carrés est n + 1 ?
-
bouyanna
- Membre Naturel
- Messages: 11
- Enregistré le: 26 Jan 2010, 01:06
-
 par bouyanna » 19 Aoû 2014, 18:01
par bouyanna » 19 Aoû 2014, 18:01
Le but c'est montrer que n+1 et la somme de trois carrés si 3n+1 est un carre
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 19 Aoû 2014, 18:02
par Shew » 19 Aoû 2014, 18:02
bouyanna a écrit:Merci pour votre reponse.
Le probléme que 3n+1 n'est pas un caré pour tous les n naturels sauf dans certaines comme 3*40+1=121=11^2 où n=40 et n+1=41=1+4+36=1^2+2^2+6^2.
On en trouve : 3*1 + 1 = 4; 3*5 + 1 = 16; 3*8 + 1 = 25

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 19 Aoû 2014, 18:09
par Ericovitchi » 19 Aoû 2014, 18:09
Supposons que 3n+1 = s². Il est clair que s n'est pas un multiple de 3, donc on peut écrire
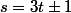
. On a alors
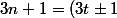^2)
et donc
^2-1}{3}=3t^2\pm2t)
donc
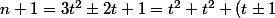^2)
:id:
-
bouyanna
- Membre Naturel
- Messages: 11
- Enregistré le: 26 Jan 2010, 01:06
-
 par bouyanna » 19 Aoû 2014, 18:17
par bouyanna » 19 Aoû 2014, 18:17
C'est tres clair et merci infiniment

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 21 Aoû 2014, 11:20
par Ericovitchi » 21 Aoû 2014, 11:20
Si s était un multiple de 3, il s'écrirait s=3k et s²=9k² serait également un multiple de 3 et ne pourrait donc pas être de la forme 3n+1 dont le reste de la division par 3 est 1.

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 21 Aoû 2014, 15:17
par Ericovitchi » 21 Aoû 2014, 15:17
ha non, le reste de la division par 3 de 3n+1, c'est 1 et pas 2.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 21 Aoû 2014, 16:41
par zygomatique » 21 Aoû 2014, 16:41
Ericovitchi a écrit:ha non, le reste de la division par 3 de 3n+1, c'est 1 et pas 2.
2 = -1 en base 3 ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 85 invités
