Logique récurrence
13 messages
- Page 1 sur 1
Logique récurrence
Pouvez vous m'aider à résoudre cet exercice :
Montrez par récurrence
Pour tout x appartenant à N tel n>=24:
Il existe au moins p,q appartenant à N² tel que
x=5p+7q
Montrez par récurrence
Pour tout x appartenant à N tel n>=24:
Il existe au moins p,q appartenant à N² tel que
x=5p+7q
Re: Logique récurrence
Bonjour,
Fixons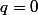 que se passe t il ?
que se passe t il ?
Nous pouvons "fabriquer" avec tous les entiers
tous les entiers  finissant par
finissant par  et
et 
Fixons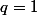 que se passe t il ?
que se passe t il ?
Nous pouvons "fabriquer" avec tous les entiers
tous les entiers  finissant par
finissant par  et
et 
Fixons ...
Conclusions : Nous pouvons fabriquer tous les entiers
Fixons
Nous pouvons "fabriquer" avec
Fixons
Nous pouvons "fabriquer" avec
Fixons ...
Conclusions : Nous pouvons fabriquer tous les entiers
Re: Logique récurrence
salut
Ca doit pouvoir aller par récurrence
Pour l'initialisation
24=5*2+7*2
On suppose donc
n=5p+7q avec n>=24, p>=0 et q>=0
On a alors
n+1=5p+7q+1=5p+7q+(5*3-2*7)=5(p+3)+7(q-2)
si q-2>=0 c'est gagné
sinon
comme q>=0, on a q-2>=-2
Les cas à examiner sont q-2=-2 soit q=0 et q-2=-1 soit q=1
**************
pour q=0
n+1=5(p+3)-14
on sait que n>=24
n+1>=25
5(p+3)-14>=25
5(p+3)>=39
p>=5 soit p=p'+5 avec p'>=0
n+1=5(p'+8)-7*2=5*(p'+1)+7*3
cqfd
*******************
pour q=1
calculs analogues
Ca doit pouvoir aller par récurrence
Pour l'initialisation
24=5*2+7*2
On suppose donc
n=5p+7q avec n>=24, p>=0 et q>=0
On a alors
n+1=5p+7q+1=5p+7q+(5*3-2*7)=5(p+3)+7(q-2)
si q-2>=0 c'est gagné
sinon
comme q>=0, on a q-2>=-2
Les cas à examiner sont q-2=-2 soit q=0 et q-2=-1 soit q=1
**************
pour q=0
n+1=5(p+3)-14
on sait que n>=24
n+1>=25
5(p+3)-14>=25
5(p+3)>=39
p>=5 soit p=p'+5 avec p'>=0
n+1=5(p'+8)-7*2=5*(p'+1)+7*3
cqfd
*******************
pour q=1
calculs analogues
Re: Logique récurrence
Salut,
ça me semble plus simple de rédiger en écrivant que, si n=5p+7q
alors n+1=5p+7q+(3*7-5*4)=5(p-4)+7(q+3)
mézossi n+1=5p+7q+(5*3-2*7)=5(p+3)+7(q-2)
donc, si p>=4 ou bien si q>=2, c'est O.K.
Et, si on n'a ni l'un, ni l'autre, c'est que p<=3 et que q<=1 donc que n<=5x3+7x1=22.
ça me semble plus simple de rédiger en écrivant que, si n=5p+7q
alors n+1=5p+7q+(3*7-5*4)=5(p-4)+7(q+3)
mézossi n+1=5p+7q+(5*3-2*7)=5(p+3)+7(q-2)
donc, si p>=4 ou bien si q>=2, c'est O.K.
Et, si on n'a ni l'un, ni l'autre, c'est que p<=3 et que q<=1 donc que n<=5x3+7x1=22.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Logique récurrence
Bonsoir,
Dans la continuité du sujet, il me semble qu'à partir d'un certain rang, tout entier peut s'écrire sous la forme
peut s'écrire sous la forme 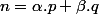 ou
ou  et
et  sont deux entiers naturels premiers entre eux et ou
sont deux entiers naturels premiers entre eux et ou  et
et  sont deux entiers naturels
sont deux entiers naturels 
Dans la continuité du sujet, il me semble qu'à partir d'un certain rang, tout entier
Re: Logique récurrence
Effectivement, si a et b sont deux entiers naturels premiers entre eux, alors tout entier naturel n>=(a-1)(b-1) peut s'écrire sous la forme n=pa+qb avec p et q entiers naturels et par contre (a-1)(b-1)-1=ab-a-b ne peut pas s'écrire sous cette forme.
Si on a fait un peu d'arithmétique (i.e. si on connait le théorème de Bézout), c'est assez facile à démontrer.
Par contre avec 3 entiers (i.e. pour a,b,c fixés, quel est le plus grand entier ne pouvant pas s'écrire n=pa+qb+rc avec p,q,r positifs) voire plus, on ne connait pas de formule simple : sauf erreur, c'est ce que l'on appelle "le problème de Frobenius" (<- orthographe incertaine...)
Si on a fait un peu d'arithmétique (i.e. si on connait le théorème de Bézout), c'est assez facile à démontrer.
Par contre avec 3 entiers (i.e. pour a,b,c fixés, quel est le plus grand entier ne pouvant pas s'écrire n=pa+qb+rc avec p,q,r positifs) voire plus, on ne connait pas de formule simple : sauf erreur, c'est ce que l'on appelle "le problème de Frobenius" (<- orthographe incertaine...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Logique récurrence
Ben314 a écrit:Salut,
ça me semble plus simple de rédiger en écrivant que, si n=5p+7q
alors n+1=5p+7q+(3*7-5*4)=5(p-4)+7(q+3)
mézossi n+1=5p+7q+(5*3-2*7)=5(p+3)+7(q-2)
donc, si p>=4 ou bien si q>=2, c'est O.K.
Et, si on n'a ni l'un, ni l'autre, c'est que p<=3 et que q<=1 donc que n<=5x3+7x1=22.
Bien vu.
A noter qu'on ne peut pas écrire n=23 sous la forme 5p+7q
Re: Logique récurrence
Oui, et ça peut éventuellement être un bon exemple pas trop capillotracté (*) où l'hérédité fonctionne à partir d'un certain rang (ici, ça marche à partir de n=23) mais où l'initialisation ne marche pas pour ce rang là.
(*) Cet adjectif EST dans le dictionnaire !!! (en tout cas dans le Petit Robert depuis 2015)
P.S. Par contre, je constate avec regrets que le nom fort usité de capillotétratomie n'y est toujours pas...
(*) Cet adjectif EST dans le dictionnaire !!! (en tout cas dans le Petit Robert depuis 2015)
P.S. Par contre, je constate avec regrets que le nom fort usité de capillotétratomie n'y est toujours pas...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Logique récurrence
et qu'est-ce que la capillotétratomie ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Logique récurrence
oui et non.... :
C'est un terme usité par tout bon xyloglotte comme synonyme du terme tétrapilectomie utilisé dans le fameux livre "Comment voyager avec un saumon" d'Umberto Eco.
C'est un terme usité par tout bon xyloglotte comme synonyme du terme tétrapilectomie utilisé dans le fameux livre "Comment voyager avec un saumon" d'Umberto Eco.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Logique récurrence
merci ben ...
sympa ta réponse qui conduit à de nouvelles questions dont la réponse est dans ta réponse !!!

sympa ta réponse qui conduit à de nouvelles questions dont la réponse est dans ta réponse !!!

Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
