Logarythme et exponentielle
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
aeris
- Membre Naturel
- Messages: 92
- Enregistré le: 10 Jan 2013, 14:53
-
 par aeris » 31 Jan 2013, 13:31
par aeris » 31 Jan 2013, 13:31
Bonjour, j'aurais besoin d'un petit coup de main pour savoir si je ne me suis pas trop planter dans mon devoir, car j'avoue avoir des doutes, quelqu'un pourrais me dire si je fais fausse route ?
Exo I : Simplifier les expressions suivantes :
A= (e^(x)-4)(1+4e^(-x))+16e(-x)
mon résultat : e^(x)
B= ln(9e(2x))-2ln(3e(x-1))
mon résultat : 4x-1
Exo II : Résoudre les équations suivantes :
A=e^(2)*e^(x^2)-e^(x^3)=0
mon résultat : x1=1 et x2=2
B=(3e^(x)-1)/(e^(x)+1)=2
mon résultat : x=-(1/4)
C=ln(x+2)+ln(x+4)=ln(x+8)
mon résultat : x1=0 et x2=5
D=2ln(x-2)=ln(-x+14)
mon résultat : ... (le "2ln" me bloque)
Exo III : Calculer la dérivée :
A=(x^2+2x-2)*e^(-x)
mon résultat : x^(2)*e^(-x)
B=(e^(-x)+1)/(e^(x))
mon résultat : (-1-2e^(x))/(e^(x)^2)
C=(x^2+1)*(ln(x^2+1))
mon résultat : 2ln(x^2+1)+2x
D=(ln(2x)+1)/x
mon résultat : (x-ln(2x)+1)/x
Exo IV : Calculer les limites
A) lim+oo (x^(2)+1)*(e^(-x))
mon résultat : 0
B) lim -oo (x^(2)+1)*(e^(-x))
mon résultat : 0
C) lim +oo (x^(2)-2)*(lnx)
mon résultat : +oo
D) lim 0+ (x^(2)-2)*(lnx)
mon résultat : -oo
Merci beaucoup d'avance !
-
aeris
- Membre Naturel
- Messages: 92
- Enregistré le: 10 Jan 2013, 14:53
-
 par aeris » 31 Jan 2013, 14:15
par aeris » 31 Jan 2013, 14:15
Personne ne peut m'aider?
-
Cheche
- Membre Rationnel
- Messages: 650
- Enregistré le: 17 Avr 2009, 19:25
-
 par Cheche » 31 Jan 2013, 14:53
par Cheche » 31 Jan 2013, 14:53
Salut :):) Il y a possibilité que tu utilises Tex plz car ce n'est pas très lisible.
Je prends le temps de te répondre ne t'inquiète pas.
-
aeris
- Membre Naturel
- Messages: 92
- Enregistré le: 10 Jan 2013, 14:53
-
 par aeris » 31 Jan 2013, 14:55
par aeris » 31 Jan 2013, 14:55
merci beaucoup!
Que j'utilise quoi ?
-
Cheche
- Membre Rationnel
- Messages: 650
- Enregistré le: 17 Avr 2009, 19:25
-
 par Cheche » 31 Jan 2013, 14:56
par Cheche » 31 Jan 2013, 14:56
Les balises Latex pour écrire les formules mathématiques.
-
aeris
- Membre Naturel
- Messages: 92
- Enregistré le: 10 Jan 2013, 14:53
-
 par aeris » 31 Jan 2013, 15:01
par aeris » 31 Jan 2013, 15:01
Cheche a écrit:Les balises Latex pour écrire les formules mathématiques.
je ne sais pas comment faire... :/
-
aeris
- Membre Naturel
- Messages: 92
- Enregistré le: 10 Jan 2013, 14:53
-
 par aeris » 31 Jan 2013, 15:03
par aeris » 31 Jan 2013, 15:03
ha si! dsl je n'avais pas remarqué "TEX"
tu préfères que je réécrive l'énoncé avec?
-
aeris
- Membre Naturel
- Messages: 92
- Enregistré le: 10 Jan 2013, 14:53
-
 par aeris » 31 Jan 2013, 15:07
par aeris » 31 Jan 2013, 15:07
-
Cheche
- Membre Rationnel
- Messages: 650
- Enregistré le: 17 Avr 2009, 19:25
-
 par Cheche » 31 Jan 2013, 15:12
par Cheche » 31 Jan 2013, 15:12
oui, si possible. C'est plus jolie pour les yeux de chacun :)
-
aeris
- Membre Naturel
- Messages: 92
- Enregistré le: 10 Jan 2013, 14:53
-
 par aeris » 31 Jan 2013, 15:13
par aeris » 31 Jan 2013, 15:13
Exo I : Simplifier les expressions suivantes :
A=
(1+4e^-^x)+16e^-^x)
mon résultat :

B=
-2ln(3e^x^-^1))
mon résultat :

-
aeris
- Membre Naturel
- Messages: 92
- Enregistré le: 10 Jan 2013, 14:53
-
 par aeris » 31 Jan 2013, 15:15
par aeris » 31 Jan 2013, 15:15
Exo II : Résoudre les équations suivantes :
A=
(e^x)^2-(e^x^)^3)=0)
mon résultat :

B=
/(e^x+1)=2)
mon résultat :
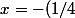)
C=
+ln(x+4)=ln(x+8))
mon résultat :

D=
=ln(-x+14))
mon résultat : ... (le "2ln" me bloque)
-
Cheche
- Membre Rationnel
- Messages: 650
- Enregistré le: 17 Avr 2009, 19:25
-
 par Cheche » 31 Jan 2013, 15:20
par Cheche » 31 Jan 2013, 15:20
ok pour la 1.
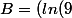 + 2x) - 2 (ln(3) + (x-1) )= 2)
-
aeris
- Membre Naturel
- Messages: 92
- Enregistré le: 10 Jan 2013, 14:53
-
 par aeris » 31 Jan 2013, 15:21
par aeris » 31 Jan 2013, 15:21
Exo III : Calculer la dérivée :
A=
*e^-^x)
mon résultat :

B=
/(e^x))
mon résultat :
/((e^x)^2))
C=
*(ln(x^2+1)))
mon résultat :
+2x)
D=
+1)/x)
mon résultat :
+1)/x)
-
aeris
- Membre Naturel
- Messages: 92
- Enregistré le: 10 Jan 2013, 14:53
-
 par aeris » 31 Jan 2013, 15:30
par aeris » 31 Jan 2013, 15:30
Exo IV : Calculer les limites
A) lim+oo
*(e^-^x))
mon résultat : 0
B) lim -oo
*(e^-^x))
mon résultat : 0
C) lim +oo
*(lnx))
mon résultat : +oo
D) lim 0+
*(lnx))
mon résultat : -oo
-
aeris
- Membre Naturel
- Messages: 92
- Enregistré le: 10 Jan 2013, 14:53
-
 par aeris » 31 Jan 2013, 15:31
par aeris » 31 Jan 2013, 15:31
Cheche a écrit: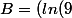 + 2x) - 2 (ln(3) + (x-1) )= 2)
J'essais de comprendre... mais je ne vois pas. tu trouves 2 en simplifiant ?
-
aeris
- Membre Naturel
- Messages: 92
- Enregistré le: 10 Jan 2013, 14:53
-
 par aeris » 31 Jan 2013, 15:36
par aeris » 31 Jan 2013, 15:36
pour exo I B, j'ai procédé comme cela :
B =
-2ln(3e^x^-^1))
B =

B =

B =

Ha j'ai trouvé ma faute!
B =

, et non B =

Ce qui donne bien
B =


-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 31 Jan 2013, 15:37
par ampholyte » 31 Jan 2013, 15:37
Bonjour,
A est faux :
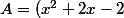*e^{-x})
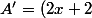 e^{-x} + -e^{-x}(x^2 + 2x - 2))
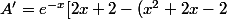])
B est faux :
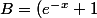/(e^x))
}{e^{2x}})

C est faux :
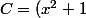*(ln(x^2+1)))
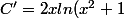 + \frac{2x}{x^2+1})
D est faux :
 + 1}{x})
* \frac{2}{2x} - (ln(2x) + 1) }{x^2})
Je te laisse terminé les calculs. Je te conseille de revoir tes dérivées :
(uv)' = u'v + uv'
(u/v)' = (u'v - uv')/v²
(exp(u))' = u' * exp(u)
(ln(u))' = u' / u

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 31 Jan 2013, 15:40
par ampholyte » 31 Jan 2013, 15:40
aeris a écrit:pour exo I B, j'ai procédé comme cela :
B =
-2ln(3e^x^-^1))
B =

B =

B =

Attention aux parenthèses
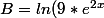-2ln(3e^{x-1}))
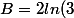 + 2x - 2ln(3) - 2(x-1))


-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 31 Jan 2013, 15:43
par ampholyte » 31 Jan 2013, 15:43
aeris a écrit:Exo IV : Calculer les limites
A) lim+oo
*(e^-^x))
mon résultat : 0
B) lim -oo
*(e^-^x))
mon résultat : 0
C) lim +oo
*(lnx))
mon résultat : +oo
D) lim 0+
*(lnx))
mon résultat : -oo
A est correctB est faux lim -oo de x² -> +oo
lim -oo de

-> +oo
donc...
C est OK
D est faux lim 0+ ln(x) -> -oo
lim 0+ x² - 2 -> -2
donc ...
-
aeris
- Membre Naturel
- Messages: 92
- Enregistré le: 10 Jan 2013, 14:53
-
 par aeris » 31 Jan 2013, 15:53
par aeris » 31 Jan 2013, 15:53
ampholyte a écrit:A est correctB est faux lim -oo de x² -> +oo
lim -oo de

-> +oo
donc...
C est OK
D est faux lim 0+ ln(x) -> -oo
lim 0+ x² - 2 -> -2
donc ...
Merci Ampholyte
donc, B) lim -oo (...) = +oo
mais je ne vois pas pourquoi D) ce n'est pas -oo ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 76 invités
