Logarithme

[rohff940000]

Je voudrais savoir comment utiliser la fonction logarithme pour trouver un entier p positif tel que 0.5^n <( 10^-5)/2 merci

[Luc69]

Je voudrais savoir comment utiliser la fonction logarithme pour trouver un entier p positif tel que 0.5^n <( 10^-5)/2 merci

il faut sans doute appliquer quelques règles simples telles que :
ln(a/b) = ln(a) - ln(b)
ln(a*b) = ln(a)+ln(b)
ln(a^b) = b*ln(a)

mais je ne vois pas où apparait p dans ton équation ???

[rohff940000]

enfaite on doit procédé par tatonement a la calculatrice car on connais pas les logarithmes,et on doit trouvé un entier p qui est égal au nombre fini dans l'intervalle de convergence [-10^-5;10^-5].Sachant qu'on doit trouver le plus petit entier p et que n est supérieur ou égal a p.Donc a la fin on trouve pour U^18 un résultat qui est environ égal a 10^-5 donc p=18 et le prof nous dit que se serait plu beaux avec un logarithme donc je veux lui faire plaisir dans mon prochain DS merci

[rohff940000]

pas de réponse aidez moi svp

[bombastus]

Bonjour,

Il faut que tu utilises les formules données par Luc69 :

Ton équation de départ, c'est :


Donc on va appliquer le logarithme à l'égalité (on peut le faire car la fonction est croissant pour des nombres positifs (croissante sur ]0+inf[)):


A ton avis, est égal à quoi? (d'après la propriété : )

[rohff940000]

n*ln(0.5) ensuite?

[bombastus]

Donc,

n*ln(0.5)à partir de là tu peux trouver l'inégalité que doit vérifier n. (pour passer ln(0,5), il faut vérifier si il est positif ou négatif pour savoir si on inverse ou pas le sens de l'inégalité)

[rohff940000]

n>ln(10^^-5/2)-ln(0.5)

c'est bien sa?

[bombastus]

Non,

(première constatation : je crois que tu as remarqué que ln(0.5)<0)

a*b<=>
a>c/b si b<0 (il faut diviser par le terme, pas le soustraire!!)

[Clembou]

Je voudrais savoir comment utiliser la fonction logarithme pour trouver un entier p positif tel que 0.5^n <( 10^-5)/2 merci

Faudrait que tout le monde réapprenne leur cours sur les exponentielles à base n... :triste:

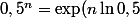[rohff940000]

n>(ln(10^-5)/2)/-ln(0.5)?

[bombastus]

@ clembou : il a précisé qu'il n'avait pas encore vu le cours sur le logarithme...

n>(ln(10^-5)/2)/-ln(0.5)

Il n'y a pas de - devant ln(0.5)!
Si tu calcules ln(0.5) avec ta calculatrice, tu trouves à peu près -0,69, c'est cela que je voulais te dire quand je t'explique que ln(0.5) est négatif. Donc dans une inégalité, lorsque l'on divise par un nombre négatif, on inverse le sens de l'inégalité, donc on obtient :
n>(ln(10^-5)/2)/ln(0.5)

[rohff940000]

ok donc n>14.28

[rohff940000]

mais p est égal a 18

[bombastus]

Tu as mal fait le calcul sur ta calculatrice, apparemment tu as utilisé 10^-4 au lieu de 10^-5...

[rohff940000]

p=17.6 c'est plus rigoureux que par tatonement

[bombastus]

Oui plus rigoureux,

Pour la fin tu obtiens :
p>17.6 (ou n, appelle le comme tu veux)
or p étant un entier, il faut choisir le premier entier qui vérifie cette inéquation donc p=18.