Bonjour à tous pouvez vous m'aider et corriger mes réponses s'il vous plais?
1 ° exo :
Soit f la fonction défénie sur [0,5 ; 3] par f(x) = ln(x) + x
On note C la courbe représentative dans le pla rapporté à un repère orthonormal.
1) Calculer f'(x)
f'(x) = 1/x +1
f'(x) = (1+x) / x
2) Etudier le sens de variation de f et donner son tableau de variation
1+x > 0
x > 1
Donc le tableau
X | 0 1 +INFINI
------------------------
F'(x)| - | +
-----------------------
F(x) | Croissante
Mais je sais pas comment l'étudier car ma courbe sur calculatrice est croissante
3)Determiner une equation de la tangeante T à C au point d'abscisse 1
Ca je ne sais pas comment faire
2° exo :
Soit f la fonction définie sur ]-1 ; +infini[ par f(x)= ln(x+1)-x
1) Calculer f'(x)
f'(x) = (1 / x +1) - 1
Je ne sais pas comment continuer a la dérivée
2) Etudier le sens de variation de f et donner son tableau de variation
Là je peut pas vu que ma dérivée est incomplète
3) Determiner le signe de f(x), pour x appartenant à ]-1 ; +infini[
Je vous remerci de votre aide et merci de m'aider.
[Term STG] Logarithme népérien
9 messages
- Page 1 sur 1
Bonsoir
Erreur. D'ailleurs, sur [0,5 ; 3], 1+x>0 et x>0 donc f '(x) ...benskateur a écrit:2) Etudier le sens de variation de f et donner son tableau de variation
1+x > 0
x > 1
Tu dois avoir dans ton cours la formule qui donne l'équation de la tangente à une courbe en un point.3)Determiner une equation de la tangeante T à C au point d'abscisse 1
Ca je ne sais pas comment faire
Salut,
on te demande d'etudier ta fonction sur [0.5;3] donc pas besoin d'aller de l'etudier sur ]0,+inf[
1) ok pour la derivée
2) comme on etdudies sur [0.5;3] on a x>0 et x+1>0 donc f'(x)=(x+1)/x>0 sur [0.5;3] donc f est croissante sur [0.5;3]
=ln(0.5)+0.5\approx{-019}) et
et 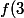=ln(3)+3\approx4.1)
d'où le tableau de variation je te laisse le faire
3 ) formule
equation de la tangente au pointd'abscisse x0 est donnée par:
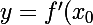(x-x_0)+f(x_0))
Soit f la fonction défénie sur [0,5 ; 3] par f(x) = ln(x) + x
On note C la courbe représentative dans le pla rapporté à un repère orthonormal.
1) Calculer f'(x)
f'(x) = 1/x +1
f'(x) = (1+x) / x
2) Etudier le sens de variation de f et donner son tableau de variation
1+x > 0
x > 1
Donc le tableau
X | 0 1 +INFINI
------------------------
F'(x)| - | +
-----------------------
F(x) | Croissante
Mais je sais pas comment l'étudier car ma courbe sur calculatrice est croissante
3)Determiner une equation de la tangeante T à C au point d'abscisse 1
on te demande d'etudier ta fonction sur [0.5;3] donc pas besoin d'aller de l'etudier sur ]0,+inf[
1) ok pour la derivée
2) comme on etdudies sur [0.5;3] on a x>0 et x+1>0 donc f'(x)=(x+1)/x>0 sur [0.5;3] donc f est croissante sur [0.5;3]
d'où le tableau de variation je te laisse le faire
3 ) formule
equation de la tangente au pointd'abscisse x0 est donnée par:
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
