Limites et valeur intermédiaire
15 messages
- Page 1 sur 1
Limites et valeur intermédiaire
Bonsoir à tous, c'est au bout de 2jour que j'abandonne ce magnifique exercice de maths :briques: . J'apprécierai votre aide. Merci d'avance :happy2:
F est une fonction définie sur R par :
f(x)= 1/2(7x^3-3x²-15x-190/49)
1)
Complétez le tableau suivant (donnez pour f(x) des valeurs approchées à 10^-3 près).
x -2 -1.5 -1 -0.5 0 0.5 1 1.5 2
f(x)
2)Montrer que l'équation f(x)=0 possède trois solutions réelles dont on donnera une valeur approchée de alpha a 10-1 près.
4)a) Déterminer trois réels a, b et c tels que, pour tout x réel, 7x^3-3x²-15x-190/49=(7x+2)(ax²+bx+c).
b) En déduire la résolution de l'équation f(x)=0.
F est une fonction définie sur R par :
f(x)= 1/2(7x^3-3x²-15x-190/49)
1)
Complétez le tableau suivant (donnez pour f(x) des valeurs approchées à 10^-3 près).
x -2 -1.5 -1 -0.5 0 0.5 1 1.5 2
f(x)
2)Montrer que l'équation f(x)=0 possède trois solutions réelles dont on donnera une valeur approchée de alpha a 10-1 près.
4)a) Déterminer trois réels a, b et c tels que, pour tout x réel, 7x^3-3x²-15x-190/49=(7x+2)(ax²+bx+c).
b) En déduire la résolution de l'équation f(x)=0.
Re
Bonjour, merci de votre aide :),
alors pour le 1. j'ai trouver des chiffres a virgules mais comme il faut donner pour f(x) des valeurs approchées à 10^-3 près je ne sais pas comment faire, par exemple si je trouve -5,5612 ce sera -5.6 ou je laisse-5,5612
2. Sur (-infini,-5/7) o est compris entre f(-infini)= infini et f(-5/7)=1.37 donc daprès le tvi, f(x)=0 admet au moins une solution sur (-infini,-5/7)
mais pour les autres solutions je ne vois pas comment les trouver même si je le vois sur la calculatrice qu'il y a bien 3, solutions pour f(x)=0
Pour le 3. j'ai trouver (7x+2)(ax²+bx+c)= 7ax^3+7bx²+7xc+2ax²+2bx+2c = 7x^3+9x²+9x+2; lorsquon enlève les lettres, mais pour identifier selon les puissances de x avec le terme de gauche comment fait on?
alors pour le 1. j'ai trouver des chiffres a virgules mais comme il faut donner pour f(x) des valeurs approchées à 10^-3 près je ne sais pas comment faire, par exemple si je trouve -5,5612 ce sera -5.6 ou je laisse-5,5612
2. Sur (-infini,-5/7) o est compris entre f(-infini)= infini et f(-5/7)=1.37 donc daprès le tvi, f(x)=0 admet au moins une solution sur (-infini,-5/7)
mais pour les autres solutions je ne vois pas comment les trouver même si je le vois sur la calculatrice qu'il y a bien 3, solutions pour f(x)=0
Pour le 3. j'ai trouver (7x+2)(ax²+bx+c)= 7ax^3+7bx²+7xc+2ax²+2bx+2c = 7x^3+9x²+9x+2; lorsquon enlève les lettres, mais pour identifier selon les puissances de x avec le terme de gauche comment fait on?
Pour le 1) arrondir au millième c'est donner 3 chiffres après la virgule (le 3e étant celui des millièmes -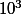 -)
-)
Pour le 2 je n'ai pas essayé mais en utilisant f' on doit pouvoir trouver différentes monotonies et en calculant les extrema de f voir qu'on trouve 3 solutions possibles.
Pour le 3 déjà il ne faut pas "enlever" les lettres ce serait pas cohérent avec ce que l'on cherche, je te donne un exemple d'identification élémentaire :
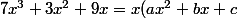)
En développant à droite on a alors :

Et par unicité de l'écriture du polynôme on en déduit :
a=7 // b=3 // c=9
Pour le 2 je n'ai pas essayé mais en utilisant f' on doit pouvoir trouver différentes monotonies et en calculant les extrema de f voir qu'on trouve 3 solutions possibles.
Pour le 3 déjà il ne faut pas "enlever" les lettres ce serait pas cohérent avec ce que l'on cherche, je te donne un exemple d'identification élémentaire :
En développant à droite on a alors :
Et par unicité de l'écriture du polynôme on en déduit :
a=7 // b=3 // c=9
Audreyk a écrit:Merci, pour le 3eme 7x^3-3x²-15x-190/49=7ax^3+7bx²+7xc+2ax²+2bx+2c quand on trouve cela on continue comment? a=7 puisqu'on le retrouve à gauche et à droite?
Ensuite on s'intéresse au système d'équation qui va égalisé les coefficients des différentes puissances de x :
7a=1
...
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
