Limites en trigonométrie TS => u(x)=(1-cosx)/(x)
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
rozie
- Membre Naturel
- Messages: 15
- Enregistré le: 13 Avr 2006, 11:49
-
 par rozie » 13 Sep 2006, 17:48
par rozie » 13 Sep 2006, 17:48
bonjour, je n'arrive pas à trouver la limite en 0 de u(x)= (1-cosx)/(x) .
J'ai fait :
pour tout x différent de 0 , -1donc -1<-cos x<1
donc 0or lim (2/x) = +l'infini et lim 0 = 0
du coup je ne trouve pas la limite de u(x)
quelqu'un pourrait-il m'aider svp?
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 13 Sep 2006, 18:04
par fonfon » 13 Sep 2006, 18:04
Salut,
}=\frac{1-cosx}{x}=-\frac{cosx-1}{x})
et utilises
}=\lim_{x\to{x_0}}{\frac{f(x)-f(x_0)}{x-x_0}})
-
rozie
- Membre Naturel
- Messages: 15
- Enregistré le: 13 Avr 2006, 11:49
-
 par rozie » 13 Sep 2006, 19:15
par rozie » 13 Sep 2006, 19:15
Merci beaucoup pour votre aide.
mais je ne comprend pas comment on fait pour passer de " u(x) est un nombre dérivé "à "lim [(1-cos(x))/x] = 0" .
pouriez-vous m'expliquer en détail ce que vous avez fait svp? Merci
ps: je viens de finir les limites mais je n'est pas encors commencé les primitifs.
-
sbz
- Membre Relatif
- Messages: 174
- Enregistré le: 01 Mai 2005, 10:00
-
 par sbz » 13 Sep 2006, 19:17
par sbz » 13 Sep 2006, 19:17
rozie a écrit:Merci beaucoup pour votre aide.
mais je ne comprend pas comment on fait pour passer de " u(x) est un nombre dérivé "à "lim [(1-cos(x))/x] = 0" .
pouriez-vous m'expliquer en détail ce que vous avez fait svp? Merci
ps: je viens de finir les limites mais je n'est pas encors commencé les primitifs.
fonfon a juste utilisé la notion de dérivabilité en un point x0 ... ta plus qu'a remplacer f(x) par (1-cos x)/x etc...
PS : tu devrais trouver 0 en limite
Bon courage
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 13 Sep 2006, 19:27
par fonfon » 13 Sep 2006, 19:27
la fonction f, est derivable en xo si,et seulement si, le taux d'accroissement:
-f(x_0)}{x-x_0})
td vers une limite finie lorsque x tend vers x0.Cette limite est le nombre derivé,noté f'(x0):
}=\lim_{x\to{x_0}}{\frac{f(x)-f(x_0)}{x-x_0})
donc dans ton exo u(x) est l'opposé du taux d'accroissement de la fonction cosinus au voisinage de 0,
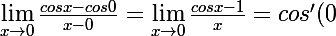=-sin(0)=0)
donc la limite recherchée est 0
A+
-
rozie
- Membre Naturel
- Messages: 15
- Enregistré le: 13 Avr 2006, 11:49
-
 par rozie » 13 Sep 2006, 19:41
par rozie » 13 Sep 2006, 19:41
merci beaucoup
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 76 invités