Limites de suite en terminale

[judith4557y89]

Bonjour
je suis bloquée sur une petite question d'un exercice depuis une heure et j'aimerais bien de l'aide. l'exercice est :
Soit (Vn ) définie par Vn=(n^3+2):(2n^2-1) déterminer la limite
j'ai trouvé (n:2)*(2n^2:2n^2-1)+(2:2n^2-1)
sauf que la limite du deuxième terme donne +l'infini quotient de +l'infini ce qui est indeterminer.
merci pour votre aide
Judith

[mathelot]

Bonsoir, factorise n^3 au numérateur et n^2 au dénominateur. Après simplification, c'est de la forme +oo. (1/2)

[judith4557y89]

je ne comprends pas je ne peut factoriser n^3 +2 avec n^3 et au dénomianteur pareil

[Pisigma]

Bonjour,

[catamat]

je ne comprends pas je ne peut factoriser n^3 +2 avec n^3 et au dénomianteur pareil

Bonjour

On peut mettre n'importe quel nombre non nul en facteur commun, il suffit de diviser les termes de la somme à factoriser par ce nombre non nul

Ex :

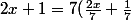Après il faut bien sûr choisir ce facteur à bon escient.

[judith4557y89]

bonjour psigma ça fait en bas + l'infini fois - l'infini ce qui fait moins l'infini comme limite et en haut +l'infini et cela nous fait encore indeterminer mais merci pour l'aide

[Pisigma]

si

[GaBuZoMeu]

Bonjour,

Le dernier signe d'égalité me semble dangereux.

[Pisigma]

Bonjour, GaBuZoMeu

oui je devrais plutôt écrire

[judith4557y89]

Pourrais tu détaillé le calcul entre le deuxième et le troisième résultat s'il te plaît

[Pisigma]

que ne comprends-tu pas la dedans?

[judith4557y89]

n^3:n^2 = n je comprends ce que je comprens est comment 2- 1:n^2 = 2-0

[Pisigma]

...






tu ne vois toujours pas?

[judith4557y89]

c'est bon merci

[Pisigma]

de rien, avec plaisir