Limites et simplification

[klink60]

Bonjour,

J'ai deux questions :

1. Limites d'une fonction
Je ne comprends pas les définitions que donne un livre sur les limites :
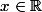
"Soit . On dit que admet pour limite en ssi tout intervalle ouvert contenant contient toutes les valeurs de pour assez grand
On note :

"
Je ne vois pas du tout à quoi cela correspond

2. Je ne comprends pas cette simplification :


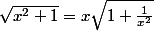
Merci de votre aide

[gol_di_grosso]

Bonjour,

J'ai deux questions :

1. Limites d'une fonction
Je ne comprends pas les définitions que donne un livre sur les limites :
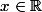
"Soit . On dit que admet pour limite en ssi tout intervalle ouvert contenant contient toutes les valeurs de pour assez grand
On note :

"
Je ne vois pas du tout à quoi cela correspond

Bonjour,
Pour 1.
On va dire que l est pas infini sinon ça va pas aller.
Fait le dessin d'une fonction qui a pour limite l dans R pas infini, puis trace la droite y=l tu prend un intervalle autour de l qu'on pourrait représenter par les droites y=l+e et y=l-e avec e dans E. Et donc si l est ta limite, il existe forcément un x à partir duquel ton graphe est toujours compris entre les deux droites précédente.
Je sens que ça va pas être clair...

2. Je ne comprends pas cette simplification :


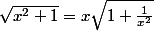
Merci de votre aide

ben disons que x différent de 0 sinon ça va pas marcher. tu factorise par
puis tu as :

[klink60]

Ok, merci.

[Flodelarab]

Je tiens à préciser (mais tout le monde l'aura remarqué) que le 2 est FAUX si x est négatif !!!

car la racine carrée de x² est égal à la valeur absolue de x et non x

[gol_di_grosso]

Je tiens à préciser (mais tout le monde l'aura remarqué) que le 2 est FAUX si x est négatif !!!

car la racine carrée de x² est égal à la valeur absolue de x et non x

hé oui :ruse: sinon il faudrais mettre une valeur absolue.