Limites première

par **emdro** » 26 Juin 2007, 16:27

J-R a écrit:pour le X2 taux de variation

Que veux-tu dire?

par **J-R** » 26 Juin 2007, 16:29

je suis d'ac pour ton calcul de rac(1-cos(x)) mais après tu me demande d'établir un quotient de 2 taux de variation?

par **emdro** » 26 Juin 2007, 16:37

On repart de

Du coup,

Le numérateur tend vers la dérivée de tan(2x) en 0, c'est à dire 2
Le dénominateur tend vers +1 (à droite) et -1(à gauche).

L'ensemble tend vers

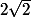
à droite et

à gauche.
La limite en 0 n'existe pas.

par **J-R** » 26 Juin 2007, 16:41

d'accord sauf qu'au 2 dénominateurs c'est 2x-0...

merci

sinon ca c'est la théorème de l'hopitale ?

par **emdro** » 26 Juin 2007, 16:44

C'est:
* (x-0) au dénominateur si on dérive tan(2x)
* (2x-0) au dénominateur si on dérive tan(x)

OK?

Oui, c'est cela la règle de l'Hospital:
Si f->0 et g->0, alors lim f/g = lim f'/g'.

par **J-R** » 26 Juin 2007, 16:45

la dérivée de tan(2x) c'est

? donc le numérateur tend vers 1

par **emdro** » 26 Juin 2007, 16:49

Non, la dérivée de f(ax+b) ce n'est pas f'(ax+b) mais af'(ax+b).

Donc la dérivée de tan(2x), c'est 2/cos²(2x). Et en 0 cela fait 2.

par **J-R** » 26 Juin 2007, 16:52

oui excuse moi c'est sans doute les vacances on va dire... :)

merci a+

par **emdro** » 26 Juin 2007, 16:53

Bonnes vacances alors!

à+

par **kiwis939** » 29 Juin 2007, 12:58

donne tous les th a connaitre

http://kiwis.miniville.fr/ind
ou bien
http://kiwis.miniville.fr

Limites première

Qui est en ligne