Limites première

par **J-R** » 26 Juin 2007, 13:25

bonjour,

je voudrais des conseils pour les limites suivantes:

merci

par **Sylar** » 26 Juin 2007, 13:49

Bonjour,pour la première en utilisant l'expression conjuguée j'obtiens:

lim I1=1

Pour la deuxième:indication:tan(2.x)=sin(2.x)/cos(2.x)........

par **J-R** » 26 Juin 2007, 13:58

pour la 1) j'arrive à:

et la 2) je suis bloquer meme avec ton indication je suis arrivé à:

par **fonfon** » 26 Juin 2007, 14:16

salut pour la 1re une idée à approfondir

à continuer en transformant ...

ps je trouve une limitequi vaut -1

par **J-R** » 26 Juin 2007, 14:26

j'ai réussi pour la première, on a un double taux de variation et on obtiens -rac(2)/2*2/rac(2)=-1

par contre l'autre....

par **J-R** » 26 Juin 2007, 14:32

non j'ai dit n'importe quoi ca tend pas vers 0....

par **J-R** » 26 Juin 2007, 15:20

c'est bon j'ai trouvé la première (avec un changement de variable)

mais pour la une je ne vois pas.... merci

par **fonfon** » 26 Juin 2007, 15:34

c'est bon j'ai trouvé la première (avec un changement de variable)

mais pour la une je ne vois pas.... merci

bizarre car si tu as réussi la premiere mais que tu ne vois pas pour la une ....

par **J-R** » 26 Juin 2007, 15:40

j'ai transformer tan(2x) multiplier par la quantité conjuguée mais...

par **J-R** » 26 Juin 2007, 15:46

je crois que j'ai trouvé ca fait 2rac(2) (j'ai pas ma calculatrice....)

par **emdro** » 26 Juin 2007, 15:50

Bonjour,

as-tu pensé à

par **emdro** » 26 Juin 2007, 15:55

bonjour,

par **emdro** » 26 Juin 2007, 16:01

Ensuite, tu fais écris le quotient de deux taux de variations.

Attention, il faut distinguer x>0 et x<0 pour enlever les valeurs absolues avant de dériver.

par **J-R** » 26 Juin 2007, 16:11

ma méthode est ce quelle marche car je ne vois pas comment introduire les 2 taux de variation avec tes données:

ma méthode:

on obtient:

}

=

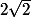
y a t-il une erreur ?

par **emdro** » 26 Juin 2007, 16:18

Il y a des = qui sont en fait des passages à la limite.

Tu as écrit que la racine du sinus² est égale au sinus. C'est la valeur absolue du sinus. Attention!

Et j'ai du mal avec la dernière étape...

par **J-R** » 26 Juin 2007, 16:20

la dernière étape je calcule l'image de 0, et c'est vrai j'ai oublié la valeur absolue...

par **emdro** » 26 Juin 2007, 16:23

Bien-sûr, suis-je bête!

Le coup de la valeur absolue, c'est important car la limite de |sinx|/x en 0 n'existe pas.

par **J-R** » 26 Juin 2007, 16:24

ah bon ?

meme en différenciant x>0 et x<0 ?

par **emdro** » 26 Juin 2007, 16:25

C'est 1 à droite et -1 à gauche.

Es-tu intéressé par ma solution avec la sin(x/2)?

par **J-R** » 26 Juin 2007, 16:25

oui mais pour le X2 taux de variation, je ne vois pas ...

Limites première

limites première

Qui est en ligne