Bonsoir à tous
J'ai des difficultés avec cette question :
Soit a un élément de Z
Calculer la limite suivante :
lim (E(x+2) + E(x-2))
x -->a+
J'ai beau me tordre les méninges, rien ne vient (J'ai presque jamais fait d'exercices avec la partie entière)
Merci d'avance pour votre aide
Limites ( Partie entière)
10 messages
- Page 1 sur 1
Salut !
Pour réel, la partie entière de
réel, la partie entière de  , notée
, notée ) ou encore
ou encore 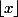 , désigne le plus le plus grand entier
, désigne le plus le plus grand entier  inférieur (au sens large) à
inférieur (au sens large) à  . Par exemple,
. Par exemple, =0) ,
, =0) ,
,  = 3) ,
, = -1) , etc...
, etc...
On peut également (puisque est archimédien) que
est archimédien) que  est strictement inférieur à
est strictement inférieur à +1) .
.
Donc en conclusion :
[CENTER]=n \Longleftrightarrow n\le x < n+1}) ,[/CENTER]
,[/CENTER]
avec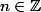 .
.
Une première propriété qui peut servir ici, c'est que quels que soient réel et
réel et  entier relatif, on a
entier relatif, on a =E(x)+p) .
.
Ensuite, de la conclusion que j'ai tirée plus haut, tu peux en déduire que la fonction "partie entière" est constante par intervalle. En effet, c'est une traduction de la conclusion : pour
est constante par intervalle. En effet, c'est une traduction de la conclusion : pour 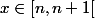 ,
, =n) donc en particulier si on remplace
donc en particulier si on remplace  par
par  , que se passe-t-il pour ta limite ?
, que se passe-t-il pour ta limite ?
Je te laisse essayer :+++:
Pour
On peut également (puisque
Donc en conclusion :
[CENTER]
avec
Une première propriété qui peut servir ici, c'est que quels que soient
Ensuite, de la conclusion que j'ai tirée plus haut, tu peux en déduire que la fonction "partie entière"
Je te laisse essayer :+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Merci pour ton aide !
Je n'ai pas bien recopié l'énoncé désolé :mur:
C'est E(x+2) + E(2-x)
En prenant en considération ce que tu m'a dis :
lim E(x+2)+E(2-x) = lim E(x) + 2 + E(-x) + 2
x->a+ x->a+
On pose x = a+h tq 0
Alors
lim E(x+2)+E(2-x) = lim E(a+h) + 2 + E(-a-h) +2
x->a+ h->0+
= lim a + E(h) -a +E(-h) + 4
h->0+
On a :E(h) = 0 et E(-h) = -1 (car 0
x->a+
= 3
:hein:Il y a pas d'erreurs ? :hein:
Merci!
Je n'ai pas bien recopié l'énoncé désolé :mur:
C'est E(x+2) + E(2-x)
En prenant en considération ce que tu m'a dis :
lim E(x+2)+E(2-x) = lim E(x) + 2 + E(-x) + 2
x->a+ x->a+
On pose x = a+h tq 0
Alors
lim E(x+2)+E(2-x) = lim E(a+h) + 2 + E(-a-h) +2
x->a+ h->0+
= lim a + E(h) -a +E(-h) + 4
h->0+
On a :E(h) = 0 et E(-h) = -1 (car 0
x->a+
= 3
:hein:Il y a pas d'erreurs ? :hein:
Merci!
Ok, +E(2-x) = E(x) + E(-x) + 4) .
.
1) Sachant que pour tout réel ,
, \le x < E(x)+1) , montre que
, montre que +E(-x) \le 0) .
.
2) Déduis-en qu'alors+E(-x)) ne peut prendre que deux valeurs possibles.
ne peut prendre que deux valeurs possibles.
3)a) Pour , que vaut
, que vaut +E(-x)) ?
?
b) Pour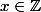 , que vaut
, que vaut +E(-x)) ?
?
:+++:
1) Sachant que pour tout réel
2) Déduis-en qu'alors
3)a) Pour
b) Pour
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Ok, +E(2-x) = E(x) + E(-x) + 4) .
.
1) Pour , que vaut
, que vaut +E(-x)) ?
?
2) Pour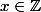 , que vaut
, que vaut +E(-x)) ?
?
:+++:
1) Pour
2) Pour
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
C'est ça, quel que soit  ,
,  + E(2-x)) =\lim_{x\to a \\ x>a} (E(x) + E(-x) )+4 =3)
:+++:
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
De rien, n'hésite pas à repasser au cas où :lol3:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
