Limites,courbes, second degré, identification

[melitssa]

bonjour,
j'aimerais un peu d'aide sur un exercice.

f est la fonction définie sur R-{3} par f(x)=x/x-3
C est la représentation graphique de f dans un repère.

1) Etudiez la limite de f en + l'infini, en - l'infini et en 3.
J'ai trouvé +l'infini pour limite en + l'infini, - l'infini pour limite en - l'infini et une forme indéterminée pour limite en 3. Je ne sais pas si c'est correct.

2)Démontrez que C a des asymptotes dont vous donnerez des équations cartésiennes.
Je n'ai pas du tout compris et je ne sais pas comment faire.

merci.

[Sdec25]

Salut
Pour trouver la limite en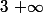 et factorise par x, on trouve 1 pour les 2 limites.

La limite en 3 est du même type que la limite de 1/x quand x tend vers 0.

Pour les asymptotes : quand limite à l'infini est finie et vaut a -> asymptote horizontale y=a
Quand la limite en a vaut l'infini, asymptote horizontale d'équation x=a

[melitssa]

merci beaucoup de m'avoir aidé. J'ai tout compris sauf pour la factorisation de x en +et - l'infini.

[Sdec25]

de rien :we:
ce qui permet de trouve facilement la limite en + et - l'infini

[melitssa]

merci je pense avoir compris cette fois .