Limites : je comprend rien !

par **Anonyme** » 14 Jan 2006, 15:11

bjr je comprend pas cet exercice(mais ca ne veut psa dire que je veux pas comprendre , bien au contraire) :

f(x) = (;)1+x) (1+ x/2) = Epsilon

En prenant lexpression conjuguée de f(x), montrer que f (x) peut sécrire sous la forme :
f(x) = x (x) avec lim (x)=0.

2. En déduire lim [(;)1+x) (1+ x/2)] / x
x->0

3. Déterminer lim [(;)1+x) 1] / x
x->0

4. Peut on déterminer avec la méthode précédente lim [(;)1+x)-1] / x² ?

Deja c'est quoi l'expression conjuguée ? et comment démontrer cela?
merci de m'avancer dans tout ca je suis perdu..

par **Anonyme** » 14 Jan 2006, 15:16

lol
tu comprends rien parce que t'es con....pffffllll

par **Anonyme** » 14 Jan 2006, 15:20

On ne juge pas une personne sur cela! Je trouve ca débile , calme vite ton comportement ...c'est pas un défouloir ici.Merci.

par **Nightmare** » 14 Jan 2006, 15:22

Qui est vraiment le plus con, celui qui ne comprend pas, ou celui qui le traite de con ? Médite sur tes paroles Houada, il ne me semble pas que tu sois capable de résoudre tout les problèmes de maths sur cette planète et vu leurs diversité je suis sûr que tu ne serais même pas capable de comprendre 1 dixiéme d'entre eux. Je ne pense pas que tu sois con pour autant.

par **Anonyme** » 14 Jan 2006, 15:22

tout a fait.. cependant quelqu'un pourrait m'aider svp ? :p

par **Nightmare** » 14 Jan 2006, 15:24

Nicoss > la quantité conjuguée de (a-b) est (a+b), le produit des deux donnant a²-b²
On utilise cela pour "supprimer" les racines carrées.

Essaye de multiplier f(x) par

par **Anonyme** » 14 Jan 2006, 15:27

J'ai oublié : lim (x)=0.
x->0

Cependant je ne vois toujours pas malgré ton aide..

par **Alpha** » 14 Jan 2006, 15:34

Nightmare a écrit:tu ne serais même pas capable de comprendre 1 dixiéme d'entre eux.

Je suis bien d'accord, et tu es même très généreux en parlant d'un dixième. Pour ma part, bien qu'étant en MP*, je crois que cela doit se situer plutôt en-dessous de 1/100 ème. Les maths sont si vastes!
Et je condamne l'intervention de houada.

A part ça, pour le problème, comme l'a dit Nightmare, en multipliant "en haut et en bas" par la quantité conjuguée, en utilisant le fait que (a-b)(a+b)a²-b², on fait sauter les racines, et on se retrouve avec un dénominateur dont la limite est facile à calculer. C'est une méthode classique qu'il faut retenir pour se débarasser des "formes indéterminées" quand on a des racines carrées.

A+

par **Anonyme** » 14 Jan 2006, 15:58

Ouais je vois comme ca, mais incapable de faire l'opération pouvez vous me l'expliquer si c'est pas trop demandé ?
Merci

par **Nightmare** » 14 Jan 2006, 16:00

Ce n'est pas compliqué

dans notre cas, qui est a, et qui est b ?

par **Anonyme** » 14 Jan 2006, 16:01

a= (;)1+x)
b= (1+ x/2)

?

par **Nightmare** » 14 Jan 2006, 16:04

Oui c'est ça

donc que vaut a² et b² ?

par **Anonyme** » 14 Jan 2006, 16:05

a= (;)1+x)²
b= (1+ x/2)²

?

par **Nightmare** » 14 Jan 2006, 16:05

Oui, c'est à dire ?

par **Alpha** » 14 Jan 2006, 16:05

Oui, c'est ça! Essaie, tu vas voir que ça marche! En prenant les a et b que tu as posés, ton expression est a-b. Maintenant, il ne te reste plus qu'à écrire que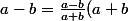

. Ensuite, en utilisant le fait que

, tu te retrouves avec au numérateur une expression dont il est facile de déterminer la limite, et celle du dénominateur est facile aussi.

Alpha+

par **Anonyme** » 14 Jan 2006, 16:10

(;)1+x)²-(1+ x/2)² ca me donne....

Mais je vois pas trop pourquoi faire ca!

par **Anonyme** » 14 Jan 2006, 16:11

enfin je vois pas le rapport avec f(x) = x (x)..

par **Alpha** » 14 Jan 2006, 16:18

Tu ne connais donc pas la définition de la racine carrée? (racine (1+x))² = 1+x !!! Développe tout, et tu verras que tu pourras factoriser un x un numérateur! Et que la fonction qui restera correspondra à ton epsilon(x)! Il faut mettre la main à la pâte un peu! Une expression, ça se développe, ça se factorise, ça se travaille un minimum, surtout dans des calculs de limite. Surtout qu'ici, il n'y a pas grand chose à faire. Ca fait partie des réflexes qu'il faut absolument avoir.

par **Anonyme** » 14 Jan 2006, 16:22

(;)1+x)²-(1+ x/2)² = 1+x - 1 + x/2 = x (1+ 1/2)

Je me rapproche? ou toujours pas?

Désolé , je comprend vite , mais il faut m'expliquer longtemps.

par **Alpha** » 14 Jan 2006, 16:26

Nicoss a écrit:En prenant l;)expression conjuguée de f(x), montrer que f (x) peut s;)écrire sous la forme :
f(x) = x (x) avec lim (x)=0.

2. En déduire lim [(;)1+x) (1+ x/2)] / x
x->0

La 1ère question est là pour que tu puisses répondre à la 2. ! Car une fois que tu as mis f(x) sous la forme voulue, dans le 2, lors du calcul de la limite, les x en haut et en bas vont se simplifier. Tu te retrouveras donc avec ton espilon(x) qui tendra vers 0 et donc la limite sera 0. L'intérêt de faire ça est de pouvoir, justement, calculer cette limite, car si tu ne touches pas ton expression du 2., tu vois une limite du type 0 sur 0, c'est à dire une forme indéterminée.

La transformation effectuée en 1 te permet de lever l'indétermination.

Alpha+

Limites : je comprend rien !

Limites : je comprend rien !

Qui est en ligne