Tu te rapproches, mais un carré, ça se développe! Tu viens quand même d'écrire que (1+x/2)² = 1 + x/2 ... Ca ne te dérange pas? Tu as oublié de développer le carré (1+x/2)²... Autre rappel : tu dois absolument savoir que (a+b)² = a² +2ab + b². Les identités remarquables (a+b)² = a² +2ab + b²,
(a-b)² = a² -2ab + b² et (a-b)(a+b) = a²-b² sont à connaître sur le bout des doigts.
A+
Limites : je comprend rien !
39 messages
- Page 2 sur 2 - 1, 2
par Nicolas_75 » 14 Jan 2006, 17:16
Je prends le fil en route, mais cela me semble faux !
(1+x/2)² = 1 + x + x²/4
(1+x/2)² = 1 + x + x²/4
par Nicolas_75 » 14 Jan 2006, 17:32
Il faut multiplier par la quantité conjuguée, comme cela t'a été indiqué ci-dessus. Je suis sûr que tu as vu des exemples de ce type en cours.
)
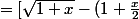]\frac{\sqrt{1+x}+(1+\frac{x}{2})}{\sqrt{1+x}+(1 + \frac{x}{2} )})
][\sqrt{1+x}+(1+\frac{x}{2})]}{\sqrt{1+x}+(1+\frac{x}{2})})
(on reconnait une identité remarquable au numérateur)
^2}{\sqrt{1+x}+(1+\frac{x}{2})})
})
})
})
)
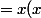en posant=\frac{-x/4}{\sqrt{1+x}+(1+\frac{x}{2})})
Et, quand
tend vers 0 :
a) le numérateur de)
tend vers 0
b) le dénominateur de tend vers 2
Donc=0)
Sauf erreur.
Nicolas
(on reconnait une identité remarquable au numérateur)
en posant
Et, quand
a) le numérateur de
b) le dénominateur de
Donc
Sauf erreur.
Nicolas
par Nicolas_75 » 14 Jan 2006, 17:43
Pour le 2. oui
Pour le 3. comment trouves-tu -1 ?
soit
: 
est dérivable sur 
et : =\frac{1}{2\sqrt{1+x}})
-r(0)}{x-0}\to r'(0)=\frac{1}{2})
Pour le 3. comment trouves-tu -1 ?
soit
par Nicolas_75 » 14 Jan 2006, 17:51
Je dois quitter le fil.
Pour la 2., ton raisonnement est incompréhensible, mais surtout semble faux. Je te rappelle que 0/0 est une forme indéterminée : on ne peut pas conclure immédiatement.
}{x}=\frac{x\vareps(x)}{x}=\vareps(x)\to 0)
Pour la 3., je pense avoir juste. Si tu as une autre méthode aboutissant à un résultat différent, poste-la. Pour ma part, j'ai simplement reconnu le taux d'accroissement d'une fonction, qui tend donc vers un nombre dérivé.
A demain,
Nicolas
Pour la 2., ton raisonnement est incompréhensible, mais surtout semble faux. Je te rappelle que 0/0 est une forme indéterminée : on ne peut pas conclure immédiatement.
Pour la 3., je pense avoir juste. Si tu as une autre méthode aboutissant à un résultat différent, poste-la. Pour ma part, j'ai simplement reconnu le taux d'accroissement d'une fonction, qui tend donc vers un nombre dérivé.
A demain,
Nicolas
par Nicolas_75 » 15 Jan 2006, 05:02
Pour la 3., je t'ai déjà expliqué deux fois. Allons-y pour une troisième.
C'est une forme indéterminée 0/0. La limite n'est donc pas immédiate. Néanmoins, on reconnait le taux d'accroissement de la fonction
, qui tend vers un nombre dérivé. Révise ton cours : c'est la définition même du nombre dérivé.
Mais tu peux également passer par la quantité conjuguée, si tu préfères. Pourquoi ne le fais-tu pas ?
(\sqrt{1+x}+1)}{x(\sqrt{1+x}+1)}=\frac{1+x-1}{x(\sqrt{1+x}+1)}=\frac{1}{\sqrt{1+x}+1}\to\frac{1}{2})
C'est une forme indéterminée 0/0. La limite n'est donc pas immédiate. Néanmoins, on reconnait le taux d'accroissement de la fonction
Mais tu peux également passer par la quantité conjuguée, si tu préfères. Pourquoi ne le fais-tu pas ?
par Nicolas_75 » 15 Jan 2006, 14:57
Pour la 4), on ne peut pas appliquer exactement la même méthode, mais on peut quand même utiliser le résultat ci-dessus.
Le premier facteur tend vers 1/2
Le second facteur tend vers +oo ou -oo
Le premier facteur tend vers 1/2
Le second facteur tend vers +oo ou -oo
par Alpha » 15 Jan 2006, 21:36
Tu verras, Nicos, avec un peu de pratique, tout cela finira par devenir évident et automatique. Poursuis tes efforts :++:
Cordialement, Alpha
Cordialement, Alpha
39 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :