Bonjour,
J'ai la correction d'un exo Yvan Monka qui dit que:
lim n>+∞ n²-n
lim n>+∞ n²=+∞
lim n>+∞ n=-∞ donc c'est une forme indéterminée.....
Pour ma part, deux choses:
Déjà on peut se dire que n² est supérieur à n donc ça tend vers l'infini
Ou alors ce que je propose n²-n=n(n-1)
lim n>+∞ de n=+∞
lim n>+∞ de n-1= +∞ donc le produit des est +∞, non??
Qu'en pensez-vous, pourquoi Yvan nous dit " forme indéterminée"??
Merci
Limite d'une suite
6 messages
- Page 1 sur 1
Re: Limite d'une suite
Bonsoir
oui, c'est une forme indéterminée, et ensuite on lève cette indétermination, en mettant n ou n² en facteur par exemple
Ton premier argument ne tient pas, x > y ne veut pas dire que la différence entre x et y devient infinie
oui, c'est une forme indéterminée, et ensuite on lève cette indétermination, en mettant n ou n² en facteur par exemple
Ton premier argument ne tient pas, x > y ne veut pas dire que la différence entre x et y devient infinie
Pour mettre une image, vous pouvez aller sur https://postimages.org/fr/
Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.

Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.
Re: Limite d'une suite
vam a écrit:Bonsoir
oui, c'est une forme indéterminée, et ensuite on lève cette indétermination, en mettant n ou n² en facteur par exemple
Ton premier argument ne tient pas, x > y ne veut pas dire que la différence entre x et y devient infinie
Je ne comprends pas ta dernière remarque : si n tend vers l’infini, pourquoi est-ce que n ²-n ne tendrait pas vers l’infini? Je ne comprends pas, pouvez-vous m’expliquer svp?
Merci
Re: Limite d'une suite
Si...mais démontre le proprement plutôt que d'affirmer
Toi tu avais dit parce que c'est supérieur
14 > 12 et pourtant 14-12 ne tend pas vers l'infini
Toi tu avais dit parce que c'est supérieur
14 > 12 et pourtant 14-12 ne tend pas vers l'infini
Pour mettre une image, vous pouvez aller sur https://postimages.org/fr/
Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.

Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.
Re: Limite d'une suite
Bonjour, autre exemple avec des suites, où n est un entier non nul

et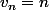
On a pour tout entier n,
mais qui pour limite zéro.
qui pour limite zéro.
et
On a pour tout entier n,
mais
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
