Limite d'une suite

[Kikoo <3 Bieber]

On veut savoir quand la fraction s'annule.

Pour cela, il suffit de voir quand le numérateur s'annule. Le dénominateur lui n'a pas le droit de s'annuler, sinon ta fraction n'a plus de sens, tu le comprends ?

[mella12]

On veut savoir quand la fraction s'annule.

Pour cela, il suffit de voir quand le numérateur s'annule. Le dénominateur lui n'a pas le droit de s'annuler, sinon ta fraction n'a plus de sens, tu le comprends ?

Ah d'accord je crois que j'ai enfin compris, merci.

[Kikoo <3 Bieber]

Tu crois avoir compris.
Si tu comprends ou non, ça te concerne, mais je veux que ce soit clair. Car il n'y a rien de pire en maths qu'une notion que l'on croit comprise alors qu'elle ne l'est pas. On retombe vite dans le flou.

Une fraction est le rapport de deux nombres.
Lorsqu'une fonction est faite d'une fraction de deux autres fonctions, on appelle communément cette fonction une "fonction rationnelle" (généralement la fraction de deux fonctions polynômiales).

Appelons toute fraction le nombre A/B
Cette fraction vaut 0 ssi A est nul et B est non nul. Pourquoi ? Parce qu'écrire A/0 n'a pas de sens, tout comme écrire 0/0 ou encore "n'importe quoi"/0.
Cela a été posé ainsi par les mathématiciens et il n'y a pas matière à discuter, c'est comme ça.

C'est pour cela que lorsqu'on étudie des fonctions rationnelles ou des quotients de fonctions (dans un sens plus général), on fait attention à éliminer de l'étude les nombres en lesquels le dénominateur s'annule. On s'occupera alors de l'intervalle (réel à ton niveau) sur lequel la fonction est définie (peut être tracée).
Pour voir quand une fonction rationnelle/(quotient de fonction) s'annule, il faut regarder quand le numérateur s'annule.

Voilà pour l'explication :happy3:

[mella12]

Oui là c'est bien compris, merci pour l'explication, et merci aussi aux autres pour leur aide.

[Joker62]

Oui j'apparais de temps en temps avec ma Patate magique qui explique tout :p

[Kikoo <3 Bieber]

Une question si Joker et sa patate magique réapparaissent par ici :)

J'ai pu voir après coup que tu disais "si... alors" alors que moi je traitais de "ssi... " en parlant de nombres qui satisfont une égalité.
Ai-je fait une faute de logique ? Pour moi il s'agissait d'une équivalence car un nombre qui satisfait une équation entraine une égalité et vice versa.
Mais maintenant que je regarde d'un peu plus près, il me semble que mon "vice versa" est bancal !
Merci de me dire si c'est bien ça qui coinçait.

[Anonyme]

@Kikoo <3 Bieber

Raisonner uniquement avec des équivalences
c'est à dire des "si et seulement si" est d'après ce que j'ai "vu" au au lycée "dangereux" !

Le risque est que beaucoup d'élèves finissent par raisonner uniquement en utilisant des équivalences
même si elles sont fausses et que seule une implication est vraie

A méditer pendant tes vacances de la Toussaint

Exemple :


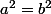
Cette équivalence peut être vraie et peut également être fausse (et cela dépend du contexte)

[Kikoo <3 Bieber]

Merci pour ta réponse daddy (cool) :)

Je vais me repencher sur mes éléments de logique. J'ai un peu honte car ça devait déjà être acquis ^^

[Anonyme]

TOUT bien acquis : ne sert à rien car on finit alors (je pense) par s'embêter !
Et il n'est jamais trop tard pour essayer d'acquérir... surtout si on est au lycée ou en prépa !

[Joker62]

Re,

On ne parlait surtout pas de la même chose.
Moi j'utilisais :

Soit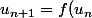 avec continue.
SI converge vers ALORS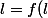

On est d'accord qu'il ne s'agit pas d'une équivalence. Il suffit de regarder l'exemple initial d'ailleurs.

Toi tu parlais d'équivalence dans la vérification d'une équation :
vérifie l'équation
Ce qui juste la définition d'une solution d'équation finalement.

Finalement, en enchaînant les raisonnements, on a :

SI converge vers ALORS vérifie

Or vérifie SI ET SEULEMENT SI SI ET SEULEMENT SI

C'est vrai que l'équivalence au lycée c'est un peu olé olé. Il est plus simple de faire de l'implication et de vérifier à la fin.
Un autre exemple d'équivalence très mal comprise :



Alors que travailler par implication est beaucoup plus direct et simple

Edit : Aurtografe

[Kikoo <3 Bieber]

Merci pour ces précisions Joker ;)

[Anonyme]

@Joker62

Il y a des exercices posés au lycée qui demandent de trouver la ou les solutions d'une équation qui n'est pas définie sur tout entier

Mais comme l'énoncé ne pose pas des questions intermédiaires du style :
Quel est le domaine d'étude (ou de définition) de cette équation
...etc....

la méthode utilisée par de nombreux prof est :
1) trouver toutes les solutions possibles de l'équation
2) vérifier que ces solutions sont bien des solutions de l'équation (dans le domaine de définition)

Moi j'ai tendance à raisonner dans "le sens inverse" ( qui me parait plus naturel )
1) définir le domaine de définition de l'équation
2) travailler dans ce domaine de définition pour trouver la ou les solutions de l'équation

car ainsi on n'a pas de vérification à faire !
sauf sur sa calculatrice :
"ce qui permet souvent de voir qu'on a fait une "boulette" au niveau de ses calculs"

Qu'en penses-tu ? Et quelle méthode préconises-tu ?

[Joker62]

Hello !

Personnellement, je pratique comme toi
Pour résoudre :

il FAUT que
Ce qui se réduit au fait qu' il FAUT que

J'ai donc déterminé dans quel ensemble mes solutions devaient tomber pour être valable.
Après, je travaille par implication :



Les solutions sont 3 et
Or seule 3 est dans le domaine des solutions donc elle est la seule possible.

On vérifie et c'est ok