Limite d'une suite - compliquée

[upium666]

Bonjour à tous et à toutes !

Cet exercice figure dans un "prise d'initiative" dans mon livre de Maths et, bizarrement, il figure dans le chapitre des intégrales, je ne vois vraiment pas trop pourquoi, voyez vous-même :


Prouver que converge et précisez sa limite
J'ai montré que converge, mais je suis vraiment bloqué pour la limite
P.S : je ne vois alors là vraiment pas pourquoi c'est dans le chapitre des intégrales :p

Merci de m'aider !

[Robic]

Bonjour à toi ! L'astuce (classique quand on la connaît, mais qui va peut-être te sembler tomber du ciel) est la suivante :
- Dessine la courbe y = 1/x.
- Entre les points d'abscisse n et n+1, l'aire de la courbe est compris entre 1/(n+1) et 1/n. Or l'aire de la courbe, c'est .
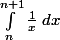
- À partir de cette remarque, tu peux encadrer par deux intégrales qu'il est ensuite possible de calculer en fonction de n. (L'une va aller de n+1 à 2n+1 et l'autre de n à 2n ou quelque chose de ce genre.)
- La limite viendra de cet encadrement.

De façon générale, quand on calcule une somme, il est souvent intéressant de la relier à une intégrale. C'est une méthode générale qu'on voit après le lycée, et en fait cette astuce n'en est pas vraiment une.