Limite d'une fonction

[k_da]

bonjour , en cours je vois les limite d'une fonction

bon voila j'essaie de comprendre mais sa ne vas pas

exercice :

lim 1-x³ / x(x²-1)
+infini

et dans mon cours la réponse donne :

lim -x³/2x³ = 1/2

pouvez vous m'expliquez comment en est on arriver la?

merci

[Joker62]

En + ou - oo, la limite d'une fraction rationnelle ( fraction de deux polynômes ) est égale à la limite en + ou - oo de la fraction rationnelle en gardant uniquement les monomes de plus haut degrés.

ici

1-x^3 => le monôme de plus haut degrés et -x^3 ( ne pas oublier le coefficient devant )

x(x^2-1) = x^3 - x => le monôme de plus haut degrés est x^3

Donc on a la limite qui est égale à lim ( +oo ) -x^3/x^3 = lim ( +oo ) -1 = -1

Donc soit ton prof s'est planté, soit t'a oublié un 2 au dénominateur. J'opte pour cette solution ;)

ATTENTION : Démarche valable uniquement en l'infini !

[k_da]

arf desolé de paraitre con , mais je pige pas :s ( sinon desolé j'ai mal recopier c'est moi

j'en dit un autre :


lim (1-x²)(3x³ -2 ) / x^6 - 5 )
-oo

la réponse = lim = -3x^5 / x^6 = 0
-oo

peut tu m'expliquer?

merci

[Joker62]

AH ben c'est sur quoi tu bloques ???
Les monômes de plus haut degrés ???

[k_da]

j'ai editer mon message

[Joker62]

Développe le numérateur...
Gardes les monômes de plus haut degrés uniquement
Et regarde la limite.

[k_da]

oki merci j'ai compris , t'a pas un exercice a me faire faire pour tester?

[Joker62]

???

[k_da]

lim 9x² / (9x-8+6 ) = a rien parce que t'a mi un trop dur mdr desolé t'a pas plus facile pour commencer?
+oo

[nico74]

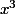
Une bonne technique est de factoriser le numerateur par le monome de plus haut degré ( dans ton 1er exo c'est ) et tu fais pareil avec le denominateur (mis sous sa forme développée). Il va donc y avoir des simplifications a faire, ce qui donne :





Or et

Donc

[nico74]

Autre exemple

Quelle est la limite en de ?





or

D'ou (J'ai un petit peu abrégé ici car c'est long décrire en latex mais tu fais limite d'une somme puis produit, blablabla...)


De plus,

Donc par produit de limites

[k_da]

merci bien mais les exercice du cours ne sont pas aussi complexe , et que se passe t-il quand il n'ya pas de division?

lim (1-10x . 3x² ) ?
+oo

[k_da]

uppppppppppp

[helene_detroie]

pour la limite en l'infini d'un polynome, tu ne te préoccupes que du terme de plus haut degré
ainsi,
lim (1-10x . 3x² ) = lim (-10x^3)= -infini
en +infini

[k_da]

je comprends pas pourquoi sa deviens -10 x exposant 3 ??

[helene_detroie]

Autant pour moi... je voulais dire -30x^3 (même si dans au final ca ne change rien...)

[k_da]

en fait tu garde le plus grand de chaque terme ?

tu a garder -10 x et 3x² et tu a fais la multiplication et donc -30 x ³ = +oo - oo donc - oo ?

[helene_detroie]

Euh, je suis pas sur d'etre d'accord avec ce que tu dis
l'idée c'est juste que quand tu considères une limite en l'infini d'un polynome, cela revient à considerer la limite en l'infini du terme de plus haut degré.
En l'occurence, ton polynome:
1-10x . 3x²=1-30x^3
le terme de plus haut degré, c'est -30x^3
et en +infini, lim -30x^3=-infini
donc en +infini, lim (1-10x.3x²)=lim -30x^3=-infini

[helene_detroie]

attention, ce théorème est vrai lorsque tu considères la limite en + ou - INFINI, d'un POLYNOME

[k_da]

donc alors

lim ( 3 - 5 x) le plus haut c'est -5x et donc -oo - oo sa fais +oo la réponse?
-oo

et pour lim ( 1-3x + x² + 5 x ^4 ) le plus haut c'est 5x^4 donc ca devrais faire
-oo -oo mais dans mes
réponse j'ai +oo comment sa sfais?