Bonjour à tous,
j'ai une narration de recherche à faire, et j'aimerai bénéficier de votre aide, svp.
Alors voilà l'énoncé, on a une figure qui est un cercle de rayon R avec un carré inscrit dans ce cercle, puis un cercle inscrit dans ce carré, et un carré inscrit dans ce cercle, et ainsi de suite.
Et on nous demande vers quelle limite tend l'aire totale des zones colorées (qui correspond à l'aire de chaque cercle en y enlevant l'aire du carré inscrit dans chacun de ces cercles) lorsqu'on poursuit la construction indéfiniment?
Et donc moi pour le moment, les remarques que je me suis faite sont:
- on a un cercle dans lequel il y a un carré inscrit, dans lequel il y a un cercle, dans lequel il y a un carré inscrit, etc. Et comme on cherche la limite de l'aire totale que fait la figure lorsqu'on enlève l'aire des carrés inscrits, j'ai pensé à faire un calcul pour chercher l'aire totale de cette figure en prenant (l'aire d'un cercle quelconque) - (l'aire du carré inscrit) + (l'aire du second cercle) - (l'aire du carré inscrit dans ce cercle là) .....etc, mais c'est trop long comme calcul.
-On pourrait penser que la limite de la figure est + l'infini du fait qu'on peut la reproduire indéfiniment (pas à la main bien sûr). Mais comme cette figure se reproduit indéfiniment à l'intérieur d'un cercle alors ce cercle est le majorant de la figure.
Voilà mes idées de départ, et je viens demander de l'aide et des avis surtout car il n'y a personne dans ma famille qui est branché géométrie et encore moins "limites" et étant toute seule je pense pas que je vais beaucoup avancer.
Merci d'avance!!
Limite d'une figure géométrique
8 messages
- Page 1 sur 1
Re: Limite d'une figure géométrique
salut
Vois commence ça se passe au début
Tu as un disque de rayon R.
Le plus grand carré a des diagonales de 2R, son aire est 2R²
Ce qui reste quand on enlève le carré (4 segments circulaires) a comme aire R²( -2)
-2)
Le cercle suivant a comme rayon R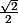
Vois commence ça se passe au début
Tu as un disque de rayon R.
Le plus grand carré a des diagonales de 2R, son aire est 2R²
Ce qui reste quand on enlève le carré (4 segments circulaires) a comme aire R²(
Le cercle suivant a comme rayon R
Re: Limite d'une figure géométrique
je ne comprends pas lorsque vous dites que le cercle suivant a comme rayon R * racine carré de 2/2
Re: Limite d'une figure géométrique
Salut,
A mon avis, pour mieux "cadrer" la discutions, tu devrait dire en quelle classe tu es, voir même (pour les andouilles comme moi qui n'ont plus aucune idée des programmes de Lycée) ce que tu connait.
Par exemple, si tu as déjà vu la notion de limite, ça pourrait être un gros "plus" (on peut évidement s'en passer, mais ça va nettement rallonger le laïus)
De même, si tu es un peu familière avec la notion d'homothétie ainsi qu'avec celle de suites géométriques, ça pourrait très nettement accélérer la compréhension du bidule.
Sinon, ça :
Ensuite, (et et encore plus dans un truc comme une "narration de recherche"), quand tu as un truc avec des points de suspension, il est souvent judicieux de calculer les premiers terme pour "voir comment ça marche" et c'est justement ce que te propose chan.
A mon avis, pour mieux "cadrer" la discutions, tu devrait dire en quelle classe tu es, voir même (pour les andouilles comme moi qui n'ont plus aucune idée des programmes de Lycée) ce que tu connait.
Par exemple, si tu as déjà vu la notion de limite, ça pourrait être un gros "plus" (on peut évidement s'en passer, mais ça va nettement rallonger le laïus)
De même, si tu es un peu familière avec la notion d'homothétie ainsi qu'avec celle de suites géométriques, ça pourrait très nettement accélérer la compréhension du bidule.
Sinon, ça :
ça me semble être un excellent début (pour ne pas dire que c'est LE début attendu...)laurence04 a écrit:...j'ai pensé à faire un calcul pour chercher l'aire totale de cette figure en prenant (l'aire d'un cercle quelconque) - (l'aire du carré inscrit) + (l'aire du second cercle) - (l'aire du carré inscrit dans ce cercle là) .....etc
Ensuite, (et et encore plus dans un truc comme une "narration de recherche"), quand tu as un truc avec des points de suspension, il est souvent judicieux de calculer les premiers terme pour "voir comment ça marche" et c'est justement ce que te propose chan.
Modifié en dernier par Ben314 le 18 Oct 2016, 12:42, modifié 5 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Limite d'une figure géométrique
laurence04 a écrit:je ne comprends pas lorsque vous dites que le cercle suivant a comme rayon R * racine carré de 2/2
Bonjour Laurence,
j'ai retrouvé ce que dit chan,
1er carré : diagonale = 2R
donc côté : (2R)² = x² + x² = 2x²
===>
aire carré =
et donc le rayon du cercle suivant, c'est la moitié du côté du carré précédent, soit (
soit
C'est vrai qu'en s'appuyant sur un schéma, même à main levée, ça aide assurément ! :
Bonne journée @ tous !
Re: Limite d'une figure géométrique
Bonjour,
alors je suis en terminale S, j'ai déjà vu les suites géométriques et une partie des limites ( pour les suites seulement, pas encore pour les fonctions).
Et merci pour le schéma, je comprends un peu mieux!!!
alors je suis en terminale S, j'ai déjà vu les suites géométriques et une partie des limites ( pour les suites seulement, pas encore pour les fonctions).
Et merci pour le schéma, je comprends un peu mieux!!!
Re: Limite d'une figure géométrique
laurence04 a écrit:Bonjour,
alors je suis en terminale S, j'ai déjà vu les suites géométriques et une partie des limites ( pour les suites seulement, pas encore pour les fonctions).
Et merci pour le schéma, je comprends un peu mieux!!!
Contents d'avoir été utiles ! @+ sur le forum.
Re: Limite d'une figure géométrique
On peut vérifier le résultat de la façon suivante:

aire de la zone rouge (les 4 parties réunies) est)
aire de la couronne (zone à l'intérieur du grand disque ET à l'extérieur du petit disque):

Le rapport A/B est égal au quotient du nombre demandé par l'aire du grand disque
demandé par l'aire du grand disque
}{\pi R^2}= \frac{x}{\pi R^2})
on doit donc trouver)
à confirmer

aire de la zone rouge (les 4 parties réunies) est
aire de la couronne (zone à l'intérieur du grand disque ET à l'extérieur du petit disque):
Le rapport A/B est égal au quotient du nombre
on doit donc trouver
à confirmer
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 71 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
