lim [x-ln(1+x)]/x²
x->0⁺
merci ;D
Limite Ln
13 messages
- Page 1 sur 1
Re: Limite Ln
par pascal16 » 06 Jan 2019, 17:40
forme indéterminée N/D
a la même limite que N'/D'
a la même limite que N"/D" qui a la chance d'exister
a la même limite que N'/D'
a la même limite que N"/D" qui a la chance d'exister
Re: Limite Ln
par pascal16 » 06 Jan 2019, 18:03
soit f(x) = ln(x+1)
f"(0) = lim en x=0 de [(f'(x+1)-f'(1))/x]
ce qui est à droite doit être ta limite à calculer
f"(0) = lim en x=0 de [(f'(x+1)-f'(1))/x]
ce qui est à droite doit être ta limite à calculer
Re: Limite Ln
par mathelot » 06 Jan 2019, 19:01
est ce que vous avez vû le calcul intégral ? (intégrales et primitives)
Re: Limite Ln
par fastandmaths » 06 Jan 2019, 21:31
Bonsoir
je ne vois pas trop ce que tu pourrais faire avec un encadrement, ..J'ai testé un taux d 'accroissement puis encore un autre par dessus le premier et franchement le résultat semble être correct (la façon d'y arriver n'est peut être pas très académique )
soit,
 } \right) \\)
et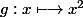
 -x } \right) -\left( 0 \right) }{ x-0 } }\times \dfrac { x-0 }{ { x }^{ 2 }-0 } =f'\left( x \right) \left( g'\left( x \right) \right) ^{ -1 })
donc encore une FI pour
Mais le truc vraiment bizarre c 'est que si je renouvelle le même procédé avec f' et g' cette fois ci en écrivant à nouveaux des taux d'accroissements:
on a
pour }^{ 2 } } }{ 2 } \longrightarrow \dfrac { 1 }{ 2 })
et sa c'est c'est juste graphiquement.
avc précaution
je ne vois pas trop ce que tu pourrais faire avec un encadrement, ..J'ai testé un taux d 'accroissement puis encore un autre par dessus le premier et franchement le résultat semble être correct (la façon d'y arriver n'est peut être pas très académique )
soit,
et
donc encore une FI pour
Mais le truc vraiment bizarre c 'est que si je renouvelle le même procédé avec f' et g' cette fois ci en écrivant à nouveaux des taux d'accroissements:
on a
pour
avc précaution
Re: Limite Ln
par mathelot » 06 Jan 2019, 22:01
nabil a écrit:Je pense qu il faut un encadrement
pour
Re: Limite Ln
par nabil » 09 Jan 2019, 21:57
ouii merci , je vais essayer de trouver le resultat par calcul integral
Re: Limite Ln
par mathelot » 09 Jan 2019, 23:26
recherche d'un encadrement:
cas x >= 0
pour
d'où
pour
dt \leq \int_{0}^x \, \frac{dt}{1+t} \leq \int_{0}^x \, (1-t+t^2)dt)
 \leq x - \frac{1}{2}x^2+\frac{1}{3}x^3)
pour
}{x^2} \leq \frac{1}{2})
cas x <= 0
pour
d'où
pour
dt \leq \int_{x}^0 \, \frac{dt}{1+t} \leq \int_{x}^0 \, (1-t+t^2-2t^3)dt)
 \leq -x + \frac{1}{2}x^2-\frac{1}{3}x^3+\frac{x^4}{2})
pour
}{x^2} \leq \frac{1}{2}-\frac{1}{3}x+\frac{1}{2}x^2)
cas x >= 0
pour
d'où
pour
pour
cas x <= 0
pour
d'où
pour
pour
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 86 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :