Limite
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
eva
- Membre Naturel
- Messages: 78
- Enregistré le: 11 Sep 2005, 18:14
-
 par eva » 21 Mar 2006, 21:44
par eva » 21 Mar 2006, 21:44
Bonsoir!
Comment calculer
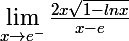
? Je n'arrive pas à enlever les formes indéterminées...
Merci de votre aide!
-
Anonyme
 par Anonyme » 21 Mar 2006, 22:11
par Anonyme » 21 Mar 2006, 22:11
sur un voisinnage )e-epsilon ; e ( ta fonction peux s'ecrire 2x/rac(e-x) *rac((1-lnx)/rac(e-x)) (sur ce vois e-x >0 ) ( * signe de multiplication )
ensuite lim (1-lnx)/e-x est le nombre dérivé de ln en e donc ...
x-->e-
ensuite compose avec racine carree ...puis suit limite d'un produit avec 2x/rac(e-x) ... sachant que e-x ----> 0+
-
Anonyme
 par Anonyme » 21 Mar 2006, 22:13
par Anonyme » 21 Mar 2006, 22:13
sauf erreur ...tu trouve + infini ...
-
eva
- Membre Naturel
- Messages: 78
- Enregistré le: 11 Sep 2005, 18:14
-
 par eva » 21 Mar 2006, 23:07
par eva » 21 Mar 2006, 23:07
si je comprends,
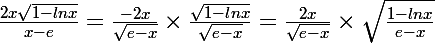
de plus,
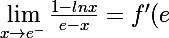 = \frac{1}{e})
et donc
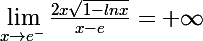
euh c'est ça? apparament oui tu as raison ça marche!
merci!
-
allomomo
- Membre Irrationnel
- Messages: 1231
- Enregistré le: 01 Mai 2005, 01:14
-
 par allomomo » 22 Mar 2006, 00:33
par allomomo » 22 Mar 2006, 00:33
Salut,
C'est faux ton résultat !
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 22 Mar 2006, 08:20
par fonfon » 22 Mar 2006, 08:20
Salut,moi je trouve -inf
-
eva
- Membre Naturel
- Messages: 78
- Enregistré le: 11 Sep 2005, 18:14
-
 par eva » 22 Mar 2006, 08:35
par eva » 22 Mar 2006, 08:35
ce serait quand même plus sympa de me dire pourquoi c'est faux! Comment fais-tu pour trouver -

fonfon?
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 22 Mar 2006, 08:57
par fonfon » 22 Mar 2006, 08:57
Re, j'ai peut-être fait une erreur mais essaie avec des valeurs proches de e par valeurs negatives dans ta fonction tu te rendra compte que ça va vers -inf
sinon
2x*sqrt(1-lnx)/(x-e)=(2x/sqrt(1-lnx))*(1-lnx)/(x-e)=-(2x/sqrt(1-lnx))*(lnx-1)/(x-e)
or comme tu l'a précisé (lnx-1)/(x-e) est le nombre dérivée de lnx en e donc
et lim-2x/sqrt(1-lnx) qd x->e- tend vers -inf donc tu n'a plus qu'à conclure en regroupant
A+
-
Anonyme
 par Anonyme » 22 Mar 2006, 09:55
par Anonyme » 22 Mar 2006, 09:55
SALUT ... exact ! limite = - infini ...j' ai ete un peu vite ... LA TECHNIQUE RESTE LA MEME sauf que sur )e-epsilon ,e( ...e-x = - (valeur absolue de e-x) car e-x negatif sur l'intervalle , ainsi e-x = - (rac(e-x))^2 ...il ya donc un facteur - de plus dans l'expression , donc - infini ( excuse moi EVA j'aurai du verifier le signe ( si A<0 alors A= - (racA)^2 ) .... A+
-
eva
- Membre Naturel
- Messages: 78
- Enregistré le: 11 Sep 2005, 18:14
-
 par eva » 22 Mar 2006, 12:38
par eva » 22 Mar 2006, 12:38
merci à vous!
-
lnk
- Membre Relatif
- Messages: 150
- Enregistré le: 11 Mar 2006, 18:33
-
 par lnk » 22 Mar 2006, 13:20
par lnk » 22 Mar 2006, 13:20
Bonjour à vous.
Je me permet de rajouter mon grain de sel mais il n'est pas précisé dans ton énnoncé Eva si il s'agit d'une limite à droite ou à gauche de e.
Par conséquent, il faut détailler les deux cas:
- l'un donnera

- l'autre

A bientôt.
Amicalement.
PS: pour enlever la forme indeterminée, décompose

en

et tu verra que le "signe de ta limite" dépent du signe de

(faire un petit tableau de signes)
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 22 Mar 2006, 13:28
par fonfon » 22 Mar 2006, 13:28
Salut, lnk je crois qu'elle le precise car elle met qd x->e- et de toute facon en e+ ce n'est pas definie car ton sqrt(1-lnx) donnera qq chose de negatif en dessous de la racine ce qui est impossible
A+
-
lnk
- Membre Relatif
- Messages: 150
- Enregistré le: 11 Mar 2006, 18:33
-
 par lnk » 22 Mar 2006, 13:30
par lnk » 22 Mar 2006, 13:30
fonfon a écrit:Salut, lnk je crois qu'elle le precise car elle met qd x->e- et de toute facon en e+ ce n'est pas definie car ton sqrt(1-lnx) donnera qq chose de negatif en dessous de la racine ce qui est impossible
A+
Exact fonfon.
Merci :++:
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 22 Mar 2006, 13:34
par fonfon » 22 Mar 2006, 13:34
Y-a pas de mal
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 86 invités