Limite de suite

[Jilbert]

Bonjour, j'ai un exercice où l'on me demande de prouver que deux suites on la même limite. Comme je peux faire ça ?
Merci

un+1=(3un+2vn)/5 et vn+1=(un+vn)/2

Où u0=16 et v0=5

Il faut prouver que l=l'
Où l est la limite de un et l' la limite de vn

[Carpate]

Bonjour,
Il faut montrer, par un raisonnement par récurrence, que :
- est décroissante
- est croissante
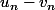- tend vers 0
alors ces 2 suites sont adjacentes et ont la même limite.
Tu n'as pas d'autres indications ?

[Jilbert]

Merci pour ces indications, non malheureusement "c'est à nous de trouver le cheminement", mais ce n'est vraiment pas simple

[Jilbert]

Mais n'ayant pas un et vn, est ce possible d'utiliser un+1 et vn+1 ?

[Black Jack]

Bonjour,

Si u(n) et v(n) > 0, alors u(n+1) = (3un+2vn)/5 et v(n+1) = (un+vn)/2 > 0
Comme u(0) et v(0) sont > 0, u(n) et v(n) > 0 pour tout n de N (1)

u(n+1) - v(n+1) = (3u(n)+2v(n))/5 - (u(n)+v(n))/2
u(n+1) - v(n+1) = (6u(n)+4v(n))/10 - (5u(n)+5v(n))/10
u(n+1) - v(n+1) = (u(n)-v(n))/10
Donc si u(n) > v(n), (u(n)-v(n))/10 > 0 et (u(n+1) - v(n+1)) > 0
Comme u(0) > v(0), on a donc u(n) > v(n) pour toute valeur de n de N (2)

u(n+1) = (3u(n) + 2v(n))/5
u(n+1) - u(n) = (3u(n) + 2v(n))/5 - u(n)
u(n+1) - u(n) = (-2u(n) + 2v(n))/5
u(n+1) - u(n) = -(2/5) * (u(n) - v(n)) < 0 (par (2))
---> la suite un est décroissante. (3)

v(n+1) - v(n) = (u(n) - v(n))/2 > 0 (par (2))
---> la suite vn est croissante. (4)

Comme un est décroissante (par 3) et minorée par 0 (par 1), la suite un est convergente.

Comme vn est croissante (par (4)) et < U(0) pour tout n de N (par (2)), vn est majorée et donc convergente.


Les suites sont convergentes, soit L la limite de u et L' la limite de v

On a alors le système :

L = (3L + 2L')/5
L' = (L+L')/2

... dont la seule solution est L = L', donc les 2 suites ont la même limite.

La valeur de L (et de L') dépend des valeurs initiales u(0) = 16 et v(0) = 5 ... mais on ne demande pas de calculer cette limite.

-----

Rien relu et donc sottises éventuelles incluses.

[vam]

Bonjour

sauf que tout le cheminement est dans le début de l'exercice
voir ici, posteur multisite, à qui on a tout mâché, mais qui ne fait rien
https://www.ilemaths.net/sujet-demonstration-par-recurrence-873565.html

[Carpate]

Variante utilisant le théorème des suites adjacentes : 2 suites adjacentes ont même limite
(2 suites sont adjacentes si l'une croit et l'autre décroit et leur différence tend vers 0)



on a donc

Supposons l'inégalité :
Montrons qu'alors :



soit



soit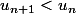
donc pour tout n :
suite croissante, suite décroissante


on a donc :


...
qui tend vers 0
et , suites adjacentes, ont même limite.

[Carpate]

Effectivement, après le signalement de ce multipost, on regrette d'avoir perdu son temps...
Est-ce que Jilbert est coutumier du fait ?