donc la définition :
Limite en un point à démontrer (trouver Lambda)
11 messages
- Page 1 sur 1
aldo56 a écrit:bonjour
je dois utiliser la définition de la limite en point pour demontrer qu'elle existe
soit la fonctionet la limite à demontrer est: limite f(x) = 7 quand x tend vers 2
donc la définition :afin de démontrer que f admet comme limite 7 au voisinage de 2
Je débute de:, d'ou j'obtiens après calcul:
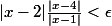
d'où:
et là je bloque
ce que je sais c'est d'arriver à identifier unen fonction de
merci pour l'aide
pose x=2+h et choisis d'abord h assez petit pour pouvoir majorer |x-4|/|x-1|
mathelot a écrit:x est voisin de 2.
On se restreint à
et
d'où(1)
la condition (1) est suffisante pour impliquer le résultat souhaité
si on choisit epsilon=1/2 donc alpha=1
est-on sur que sur ]1;3[ |f(x)-7|<1/2 ? (ex calculer f(1,5)=9,5 !!
en réalité il faut rester à l'inégalité |x-2||x-4|/[x-1| < epsilon
puis sur un petit intervalle de centre 2 et rayon h majorer |x-4|/|x-1| par k puis choisir pour alpha min(h,epsilon/k)
si x tend vers 2, on restreint l'étude des fonctions f et f' à un petit voisinage de 2.
sur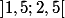 f' est bornée (uniformément) par une constante k que j'ai la flemme de calculer.
f' est bornée (uniformément) par une constante k que j'ai la flemme de calculer.
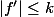 (2)
(2)
on a le droit de primitiver cette inéquation (c'est du programme Bac+1) mais je tente de t'expliquer...
-f(2) | \leq k|x-2|)
pour rendre-f(2)|) inférieur à
inférieur à  ,
,
il suffit de prendre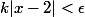
et donc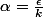 sans oublier
sans oublier 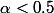
-----------------------------------------------------------------------------------------------------------
Au niveau de la logique formelle, on souhaite
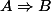
on définit telle que
telle que 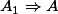 et
et 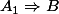 , en diminuant
, en diminuant  d'où
d'où
 \Rightarrow (A \Rightarrow B))
------------------------------------------------------------------------------------------------------------
sur
on a le droit de primitiver cette inéquation (c'est du programme Bac+1) mais je tente de t'expliquer...
pour rendre
il suffit de prendre
et donc
-----------------------------------------------------------------------------------------------------------
Au niveau de la logique formelle, on souhaite
on définit
------------------------------------------------------------------------------------------------------------
mathelot a écrit:si x tend vers 2, on restreint l'étude des fonctions f et f' à un petit voisinage de 2.
surf' est bornée (uniformément) par une constante k que j'ai la flemme de calculer.
(2)
on a le droit de primitiver cette inéquation (c'est du programme Bac+1) mais je tente de t'expliquer...
pour rendreinférieur à
,
il suffit de prendre
et doncsans oublier
-----------------------------------------------------------------------------------------------------------
Au niveau de la logique formelle, on souhaite
on définittelle que
et
, en diminuant
d'où
------------------------------------------------------------------------------------------------------------
sans passer par des th hors bac
si x]3/2;5/2[ 3/2<4-x<5/2
1/2<x-1<3/2 2/3<1/(x-1)<2
1<(4-x)/(x-1)<5
donc si alpha=min (epsilon/5,1/2) |x-2||x-4|/|x-1|<5|x-2|<epsilon
aldo56 a écrit:bonjour
désolé de revenir sur ce sujet
j'ai essayé de refaire cet exercice mais je pense que tu t'es trompé au niveau de ton encadrement;
ce que j'ai fait
je suis arrivé après calcul: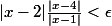
d'où:
donc l'objet, si j'ai bien compris, est de majorer :
pour l'encadrement de, j'ai suivi ton même raisonnement mais j'aboutis à un intervalle différent:
pouron a :
et donc
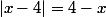
et enfin:
au final on a (|4-x| =|x-4|):
pour (x-1) on a pouravec
d'où
donc
d'où:
ce qui majore le rapport donc c'est
d'où(bien sur sauf erreur!)
merci
NON l'objet est de majorer |x-4|/|x-1|
je t'ai donné un contre exemple en choisissant epsilon=1/2 et x=1,5 on trouve f(x)=9,5 et
|f(x)-f(2)|=2,5 n'est donc pas inférieur à 1/2
aldo56 a écrit:bonjour
désolé de revenir sur ce sujet
j'ai essayé de refaire cet exercice mais je pense que tu t'es trompé au niveau de ton encadrement;
Bonjour
Je ne vois pas où Manny06 aurait fait une erreur
on peut bien choisir d'abord
Manny06 a choisi 1/2
Prenons
alors
d'une part
d'autre part
on vérifie qu'il suffit de choisir
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
