Bonjour,
Je faisais mon exercice de math tranquillement, quand je suis arriver à celui-ci qui me bloque.
Je n'arrive pas du tout à comprendre cette exercice sur les limites de fonctions exponentielles.
Quelqu'un pourrait m'aider à comprendre.
Photo de l'exercice : http://image.noelshack.com/fichiers/201 ... -titre.png
Merci de votre aide !
Limite fonctions exponentielle
4 messages
- Page 1 sur 1
Re: Limite fonctions exponentielle
par aymanemaysae » 04 Déc 2018, 11:27
Bonjour;
a)
On a :
et 
donc :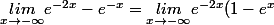=+\infty)
.
Tu peux t'inspirer de cet exercice pour résoudre l'exercice (b) .
En ce qui concerne l'exercice (c) , tu peux utiliser la méthode du conjugué .
a)
On a :
donc :
Tu peux t'inspirer de cet exercice pour résoudre l'exercice (b) .
En ce qui concerne l'exercice (c) , tu peux utiliser la méthode du conjugué .
Re: Limite fonctions exponentielle
par aymanemaysae » 05 Déc 2018, 10:46
Bonjour;
Pour la question (b) je crois que tu peux le faire maintenant .
Pour la question (c) , je détaille ci-après la méthode .
(\sqrt{e^{2x}+1}+e^{x})}{\sqrt{e^{2x}+1}+e^{x}}=\underset{x\rightarrow+\infty}{lim}\dfrac{\sqrt{e^{2x}+1}^2-e^{2x}}{\sqrt{e^{2x}+1}+e^{x}})
.
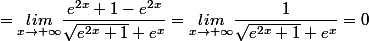J'espère que tu vas poster prochainement la solution de l'exercice (b) pour voir si tu as bien assimilé la démarche proposée .
Pour la question (b) je crois que tu peux le faire maintenant .
Pour la question (c) , je détaille ci-après la méthode .
J'espère que tu vas poster prochainement la solution de l'exercice (b) pour voir si tu as bien assimilé la démarche proposée .
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :