Limite de la fonction sqrt(x^2+2x-3)+x en -inf
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
expontiel
- Messages: 5
- Enregistré le: 05 Mar 2012, 19:16
-
 par expontiel » 05 Mar 2012, 19:22
par expontiel » 05 Mar 2012, 19:22
Bonjour
je vous savoir est ce que la limite de la fonction sqrt(x^2+2x-3)+x en -oo est : -1 ou non ?
et merci bcp mes amis
-
manoa
- Membre Relatif
- Messages: 343
- Enregistré le: 12 Oct 2011, 00:02
-
 par manoa » 05 Mar 2012, 19:29
par manoa » 05 Mar 2012, 19:29
c'est
+x)
?
bah c'est quoi la limite de
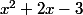
et de x en +oo
-
expontiel
- Messages: 5
- Enregistré le: 05 Mar 2012, 19:16
-
 par expontiel » 08 Mar 2012, 12:21
par expontiel » 08 Mar 2012, 12:21
:mur:
Pardon mais c'est un faut de frappe
je veux dire lim sqrt(x^2+2x-3)+x en -oo
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 08 Mar 2012, 14:24
par Carpate » 08 Mar 2012, 14:24
expontiel a écrit::mur:
Pardon mais c'est un faut de frappe
je veux dire lim sqrt(x^2+2x-3)+x en -oo
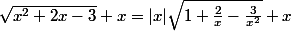
Et pour

,
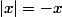
...
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 08 Mar 2012, 14:53
par Carpate » 08 Mar 2012, 14:53
Carpate a écrit: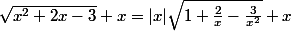
Et pour

,
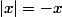
...
Erreur : ma première réponse menait à 0 * -infini !
Il faut multiplier par la quantité conjuguée :
=\sqrt{x^2+2x-3} +x = (\frac{\sqrt{x^2+2x-3} +x). (\sqrt{x^2+2x-3} -x) }{\sqrt{x^2+2x-3} -x}=<br />\frac{x^2 +2x -3 - x^2}{\sqrt{x^2+2x-3} -x}= \frac{2x-3}{\sqrt{x^2+2x-3} -x})
Et le dénonimateur devient

et

quand

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
