Bonjour, je vous envois mon énoncé et ma réponse, pouvez vous me corrigé, merci !
ÉNONCE:
On considère la fonction f définie pour tout réel x par : f(x) = xe^(1-x²)
1) calculer la limite de la fonction f en + l'infinie
Indication : on pourra utiliser pour tout réel x différent de 0,
f(x) = (e/x)(x²/e^x²)
On admettra que la limite de la fonction f en - l'infinie est égale à 0
RÉPONSE:
Limite en + l'infinie de f(x) = xe^(1-x²)
Lim 1-x² = - l'infinie
alors Lim e^(1-x²) = - l'infinie
Donc Lim xe^(1-x²)
Limite en + l'infinie de f(x) =(e/x)(x²/e^x²)
Je ne vois pas du tout comment faire
Limite fonction exponetielle
11 messages
- Page 1 sur 1
Re: Limite fonction exponetielle
Attention :
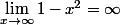 , ça c'est ok mais...
, ça c'est ok mais...
en posant X = 1-x^2,
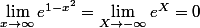
L'énoncé te fait remarquer que, quand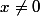 ,
,  = (e/x)(x^2/e^{x^2}))
Donc = \lim_{x \to \infty}(e/x)(x^2/e^{x^2}))
Tu n'as pas exploré cette piste.
en posant X = 1-x^2,
L'énoncé te fait remarquer que, quand
Donc
Tu n'as pas exploré cette piste.
Modifié en dernier par chombier le 13 Fév 2017, 16:25, modifié 4 fois.
Re: Limite fonction exponetielle
Borne sup, maths spé !
Re: Limite fonction exponetielle
f(x) = (e/x)(x²/e^x²) = (e*e^x²)+x^3
Alors lim (e*e^x²) = + l'infinie
et lim x^3 = + l'infinie
donc par quotient lim f(x) = + l'infinie ?
Alors lim (e*e^x²) = + l'infinie
et lim x^3 = + l'infinie
donc par quotient lim f(x) = + l'infinie ?
Re: Limite fonction exponetielle
Alfreddupapier a écrit:f(x) = (e/x)(x²/e^x²) = (e*e^x²)+x^3
Indice : il faut lever l'indétermination en utilisant une des limites de références e^x/x, x e^-x, etc.
Re: Limite fonction exponetielle
Je fais le produit en croix car avec cette écriture (e/x)(x²/e^x²) je ne parviens pas à trouver directement les limites
Re: Limite fonction exponetielle
Tu condidères que 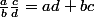 . Oublies, le produit en croix ce n'est pas ça du tout ! (Voila pourquoi il faut se méfier de ce genre d'expression, tout comme du verbe faire)
. Oublies, le produit en croix ce n'est pas ça du tout ! (Voila pourquoi il faut se méfier de ce genre d'expression, tout comme du verbe faire)
Le produit en croix te dit que SI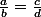 ALORS
ALORS 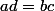
Revenons à nos moutons. Tu dois calculer et
et 
Tu dois utiliser pour cela la limite de référence :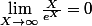
Le produit en croix te dit que SI
Revenons à nos moutons. Tu dois calculer
Tu dois utiliser pour cela la limite de référence :
Re: Limite fonction exponetielle
Lim e/x = + l'infinie
Lim x²/e^x² = lim x/e^x = 0
Mais cela revient a une forme indéterminé
Lim x²/e^x² = lim x/e^x = 0
Mais cela revient a une forme indéterminé
Re: Limite fonction exponetielle
Alfreddupapier a écrit:Lim e/x = + l'infinie
Lim x²/e^x² = lim x/e^x = 0
Mais cela revient a une forme indéterminé
Tu dois être plus précis, parles-tu de la limite en 0, en -3, en
Partons du principe que tes limites sont en
Ta première limite est fausse.
Ta deuxième limite est mal rédigée. Elle laisse sous entendre que
Re: Limite fonction exponetielle
e/x = ex/x² = ex*x^-2
Limite en + l'infinie
Lim ex = + l'infine et
lim x^-2 = - l'infinie
Donc par produit lim e/x = - l'infinie
x²/e^x² = (x²) *(e^-x²)
Limite en + l'infinie
Lim x² = + l'infinie
Lim e^-x² = + l'infinie
donc par produit lim x²/e^x²
Donc par produit lim (e/x)*(x²/e^x²) = - l'infinie
Limite en + l'infinie
Lim ex = + l'infine et
lim x^-2 = - l'infinie
Donc par produit lim e/x = - l'infinie
x²/e^x² = (x²) *(e^-x²)
Limite en + l'infinie
Lim x² = + l'infinie
Lim e^-x² = + l'infinie
donc par produit lim x²/e^x²
Donc par produit lim (e/x)*(x²/e^x²) = - l'infinie
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 95 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
