Limite de fonction à deux variables ?

[totor]

Bonjour,

je voudrais calculer la limite de




est-ce que c'est possible ???? j'ai tracé la fonction sous matlab qui a l'air de tendre vers en 0...mais je suis pas sûr...

pourriez vous m'aider ?

merci par avance

[nox]

si je ne m'abuse tout dépend de la manière dont tu fais tendre tes variables vers 0.

Pour les fonctions multi-variables il existe plusieurs types de limite :
limite directionnelle, double, successive...

[totor]

salut,

ben heu ...je savais pas :( en fait je l'utilise dans un programme ou j'ai des valeur de x et y qui varient, et a un moment elle valent toutes les deux zéros ...du coup je sais pas quelle valeur mettre :(((((((((( ?

y'aurait t-il qque part ou je puisse trouver des indications sur ce sujet ?

merci encore

[Sdec25]

Bonjour
c'est bizarre je ne trouve pas la même limite.
Tu peux essayer par encadrement.

x² / (x² + y²) > 0
x² / (x² + y²) < x² / x² = 1
Donc la fonction est comprise entre 0 et 1
Pour trouver que la limite est 1 je ne me souviens plus trop comment on fait mais je vais chercher (c'est toujours pas encadrement).

[Sdec25]

En fait il arrive que quelque soit la façon dont on fait tendre les variables, il y a une limite qu'il faut trouver par encadrement.
Quand ce n'est pas le cas la fonction n'a pas de limite.
Sous Excel je trouve une limite égale à 1.

[totor]

En fait il arrive que quelque soit la façon dont on fait tendre les variables, il y a une limite qu'il faut trouver par encadrement.
Quand ce n'est pas le cas la fonction n'a pas de limite.
Sous Excel je trouve une limite égale à 1.

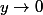
Merci ! C'est donc une limite successive, faisant d'abord tendre , puis c'est ça ?

[kazeriahm]

ta fonction n'a pas de limite en 0.

pour le prouver tu montre que tu peux faire tendre (x,y) vers (0,0) de deux manieres distinctes et obtenir deux limites distinctes.

par exemple f(0,y)=0 et ce poour tout y donc limite quand y tend vers 0 de f(0,y)=0.
f(x,x)=1/2 donc lim quand x tend vers 0 de f(x,x)=1/2 donc pas de limite.

ce raisonnemen est valable, apres la formulation est a revoir.

si il te semble qu'une fonction de deux variables converge, la meilleure maniere est d'utiliser les coordonnes polaires :
x=p*cos(a) y=p*sin(a) tu remplace (par ex x^2+y^2=p^2,etc...) et tu regarde ce qui se passe quand p tend vers 0.si cette limite est indepedante de a, alors c'est la limite de ta fonction. si ta limite depend de a, ta fonction ne converge pas puisque sa limite depend de la facon dont tu te rapproche de 0...

je sais pas si c tres clair.

[fonfon]

Salut, je ne suis plus trés sûr car longtemps que j'en ai pas fait donc a confirmer on pose :

et on remplace et on utilise le sup et on fait tendre r vers 0

[Mikou]

j'aurais pensé que la limite etait 1/2 :)

[totor]

ta fonction n'a pas de limite en 0.
je sais pas si c tres clair.

coucou,

si c'est clair ...malheureusement :p ...Alors dans ce cas je trouve, en passant en coordonées glaciales



mais en fait la limite que je cherche véritablement a calculer c'est :



dans ce cas la, par encadrement comme , je peux dire que la limite est ????


j'ai bon ?? :hein: :marteau: :mur: ??

[Sdec25]

Logiquement pour ta fonction la limite est celle de

[totor]

Logiquement pour ta fonction la limite est celle de

youpi !!

MERCI :we:

j'aurai une autre question sur les limites de fonctions à deux variables si possible .....que faire de



étant donné que tout les termes sont compris entre zéro et un ...est ce que je peut qd même calculer un limite là dessus ???


merci encore

[Sdec25]

Je ne crois pas qu'on puisse trouver une limite :

et

donc il y a plusieurs limites possibles pour le produit.

[totor]

Est ce que je peux remplacer ces fonctions par des developpements limités autour de zéro ?

[aviateurpilot]

soit ABC un triangle rectangle en A tel que
x=AB ,y=AC et a=ACB

on fait tendre x et y vers 0 de tel sorte que les triangle obtenu restent toujour semblable à ABC.
dans ce cas est constante
donc
pour ; A=1/2
pour ; A=3/4
donc pas de limite

[kazeriahm]

youpi !!

j'aurai une autre question sur les limites de fonctions à deux variables si possible .....que faire de

je persiste et je signe :we:

avec la methode citee plus haut, en posant
, il vient
donc en choisissan il vient donc limite quand r tend vers 0 egale -1,

et pour a=pi/4 par exemple, on obtient limite =l'infini

(desole la flemme de tex)

donc pas de limite comme l'a dit sdec