Bonjour à tous !
Je suis en terminale S, et j'ai un DM à rendre pour le vendredi 24/09.
J'ai quasiment tout fait, mais je bloque au dernier exercice... J'espère que vous pourrez m'aider !
Énoncé:
f est la fonction définie sur R par f(x) = x + racine de(x²+x+1).
1 - Dérivez la fonction et dressez son tableau de variations.
2 -
a) Démontrez que la droite d d'équation y= -(1/2) est asymptote à la courbe en -infini
b) Démontrez que la droite d' d'équation y= 2x+(1/2) est asymptote à la courbe en +infini
J'ai fait la question 1 sans problème, je bloque sur la 2 ..
Je sais que si y=a est une asymptote verticale, alors lim f(x) = a (question 2a)
et que si y=ax+b alors lim f(x) -(ax+b) = 0 (question 2b)
Mais j'arrive pas à démontrer que lim f(x) = -(1/2) en -infini et lim f(x) -(2x+1/2) en +infini (même avec la quantité conjuguée, à moins que j'ai fait une erreur...)
Merci d'avance pour vos réponses !
Lechero.
Limite et asymptote (Tle S)
5 messages
- Page 1 sur 1
Démontrez que la droite d d'équation y= -(1/2) est asymptote à la courbe en -infini
Il suffit de démontrer que
Pour faire ça multiplies en haut et en bas par la quantité conjuguée puis mets x en facteur en haut et en bas et ta limite ne sera plus indéterminée
(et n'oublies pas qu'un x² sort de la racine en -x car x est négatif c.a.d que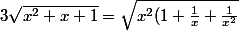}=-x\sqrt{1+\frac{1}{x}+\frac{1}{x^2}}) c'est une erreur que l'on fait souvent
c'est une erreur que l'on fait souvent
Il suffit de démontrer que
Pour faire ça multiplies en haut et en bas par la quantité conjuguée puis mets x en facteur en haut et en bas et ta limite ne sera plus indéterminée
(et n'oublies pas qu'un x² sort de la racine en -x car x est négatif c.a.d que
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
