Lim : 2x²+x-1 / x-1

[andy06]

Bonjour je voudrais savoir si la limite de 2x²+x-1 / x-1
lorsque
x -> 1
x < 1
est : Forme Imposible

x -> 1
x > 1
est : Forme Imposible

x -> +Infini
est : 0

x -> -Infini
est : 0

Car je trouve ca bisare.

Merci d'avance

edit :
un autre pobleme ^^^
a partire de f(x)= ax + b +c/x-1
j'ai trouver
f(x)= 2x+3+ 2/x-1
et f'(x) = 2 + 2/ (x-4)²

Ese que c'est ausi bon

Merci encor d'avance.

[alex.3590]

qd x tend vers 1 tu t'est trompé et pour x tend vers + ou moins infini il faut lever l'indetermination

[alex.3590]

Bonjour je voudrais savoir si la limite de 2x²+x-1 / x-1
lorsque
x -> 1
x 1
x > 1
est : Forme Imposible

qd x->1 et x<1 lim=-infini (tu as 2/ )

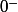
[alex.3590]

qd x->1 x>1 ça tend vers +infini

[alex.3590]

sinon pour les deux autres on a f(x)= ce qui egale [x²(2+1/x-1/x²)]/x(1-1/x)

donc on a x(2+1/x-1/x²)/(1-1/x)

et dc lim=+infini qd x tend vers + infini et -infini qd x tend vers -infini

[andy06]

et pour x tend vers + ou moins infini il faut lever l'indetermination

Comment ca??

Sinon
un autre pobleme ^^^
a partire de f(x)= ax + b +c/x-1
j'ai trouver
f(x)= 2x+3+ 2/x-1
et f'(x) = 2 + 2/ (x-4)²

Ese que c'est ausi bon

Merci encor d'avance.

[alex.3590]

Comment ca??

c'est expliqué apres :happy2:
sinon att pour l'autre pb je regarde

[alex.3590]

ton autre pb consiste a trouver a b et c c'est ça??

[alex.3590]

si c'est le cas tu fais ax+b+c/(x-1)=[(ax+b)(x-1)+c]/x-1

=(ax²-ax+bx-b+c)/(x-1)
=(ax²+x(b-a)-b+c)/(x-1)

et tu procedes par identification

[andy06]

J'ai trouver
a=2
b=3
c=2
(J'espere que c'est ca)

Mais apres le la deriver que je suis pas sure.

[alex.3590]

pour a,b et c c'est bon quant a la derivée je regarde

[alex.3590]

c'est f'(x)=2-2/(x-1)²

[andy06]

ok

merci j'ai refait je trouve comme toi

Encore merci :we:

@+