Ligne de niveau

[moi159]

Bonjour , j'aurai re besoin d'aide pour un exo que je ne comprends pas :

On donne

Un segment [AB] de longeur 4 . On se propose de determiner l'ensemble des points M du plan tels que vect AB . ( scalaire) AM = 12 , appelé ligne de niveau 12 et noté L12.

1) Soit H projeté orthogonal de point M sur la droite ( AB)

Démontrer que vect AB.AM=12 et AB.AH = 12

J'ai réussi

2) En déduire que la ligne de niveau 12 et une droite que l'on précisera
La tracer

j'ai aussi réussicar j'ai trouvé que AB fois AH = 12

donc AH= 3

mais je ne vois pas du tout comment la tracer ^^

3 ) Par la meme méthode déterminer, puis tracer sur la meme figure , les lignes de niveau L24 et L-8. Quelle est la ligne de niveau 0

Pour determiner dois je utiliser par ex : AB.AH = 24 ???

La ligne de niveau 0 est telle que AB perpendiculaire à AH

4) Determiner K pour que la ligne Lk soit la médiatrice de [AB] , je bloque completement ici



merci beaucoup d'avance

[uztop]

Bonjour,

Pour la question 2, les points M sont tels AH=3 comme tu l'as dit
Tu peut donc facilement placer le point H; quels sont tous les points dont le projete orthogonal est H ?

3) Oui, c'est exactement ca: il faut trouver tous les points M tels que AB.AH = 24 et ensuite tels que AB.AH = -8
Pour 0, tu peux dire un peu mieux: tu sais que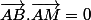 , que signifie que le produit scalaire de deux vecteurs est nul ?

4) Quand tu aurais repondu aux autres questions, ca devrait etre facile

[moi159]

pour la 2 )

c'est une droite orthogonale en H à [AB]

3) pour L 24 , je trouve que AH = 6 , c'est donc pareil que pour la 2) mais le point H est décallé. Pour L-8, je trouve une longeur négative , c'est donc impossible

et pour 0, on peut dire que comme AB. AM= 0 , AB est donc perpendiculaire à AM

4) je ne vois vraiment pas comment faire ! dois je utiliser le fait que le point m est équidistant de A et de B ?

[uztop]

3) L=-8 est possible. En effet, on parle de produits scalaires, les vecteurs ont donc bien une direction.
Il faut trouver H tel que AB.AH=8 et que les vecteurs et 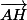soient de direction opposee.
Ensuite, pour la ligne de niveau 0, oui c'est bon, il faut donc dire le ligne de niveau est la perpendicullaire a (AB) passant par A

4) Oui, M est equidistant a A et B, mais on sait aussi que H (le projete orthogonal de M) est equidistant a A et B; tu sais donc que AH=AB/2, tu devrais pouvoir trouver k assez facilement

[moi159]

est ce que la 2 ) est bonne ???

Donc pour L-8 , le point H est en dehors du segment AB ?


pour la 4 ) j'a trouvé que K = 8 ?

[uztop]

oui, oui et oui :)

[moi159]

merciiii beaucoup !!!!!!!!!!!!