"Sur un graphique que repésentent
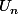
et

"
Evidement, tout dépend du graphique...
Vu l'exo, je ferais bien un graphique avec un axe des x, un axe des y et la courbe de la fonction
=\sqrt{1+x})
.
A priori, au début, vu que
)
je mettrait bien

sur l'axe des x et

sur l'axe des y pour 'voir' l'égalité
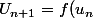)
.
Sauf que, dans la partie dont tu parle (la récurrence), pour comprendre, il vaut mieux 'voir'

et

sur l'axe des x puis
)
et
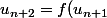)
sur l'axe des y.
"f est strictement croissante car
=sqrt{1+x})
?"
bien sûr !!!
"pourquoi si f est strictement croissante, et

alors la suite est décroissante ?"
Là tu mélange 2 choses :
Le fait que f est croissante permet de faire la réccurence : "si

alors
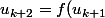<f(u_k)=u_{k+1})
"
Aprés, une fois la réccurence "finie", on en déduit (de la réccurrence) que
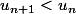
pour tout n naturel et cela prouve (c'est la définition) que la suite est décroissante
