Les nombres complexes à l'aide!

[Carpate]

z²-2z+4+4i=0 a une solution imaginaire pur , soit k.i avec k réel cette solution.

On a donc : k²i² - 2ki + 4 + 4i = 0
-k²+4 + i(4-2k) = 0

Et donc k doit être solution du système;
-k²+4 = 0
4-2k = 0

La seule solution est k = 2

La solution imaginaire de (F) est donc z = 2i

Donc z²-2z+4+4i est divisible par (z - 2i)

z²-2z+4+4i = z²-2iz + 2iz + 4 -2z + 4i = z(z-2i) + 2i(z - 2i) - 2(z - 2i)

z²-2z+4+4i = (z-2i).(z + 2i - 2)

Les solutions de (F) sont donc z1 = 2i et z2 = 2 - 2i

:zen:

C'est bien !
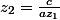
Et si tu es pressé par le temps dans un exercice, souviens-toi que la méthode de calcul de l'autre racine quand on en connaît une est plus rapide que celle par identification.

[Carpate]

Par exemple, à un signe près je pense.

Ou bien montrer que |AC| = |AB|

:zen:

Oui, les arguments sont opposés.
Les 2 méthodes sont équivalentes.

[Carpate]

Par exemple, à un signe près je pense.
Les arguments sont de signes contraires
Ou bien montrer que |AC| = |AB|

:zen:

Les 2 méthodes sont équivalentes.

J"avais pas vu que la suite des messages étaient sur une autre page !

[Black Jack]

C'est bien !
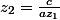
Et si tu es pressé par le temps dans un exercice, souviens-toi que la méthode de calcul de l'autre racine quand on en connaît une est plus rapide que celle par identification.

Je n'utilise jamais la méthode par identification, inutilement longue, mais qui aide actuellement où on préfère enseigner des routines que privilégier le raisonnement.

Soit j'utilise la méthode de mon message précédent, imbattable en vitesse d'exécution, soit j'utilise la division de 2 polynomes (fussent-ils à coefficients complexes) comme on l'enseignait jadis et c'est tout aussi immédiat.

:zen:

[kapelaony]

Par exemple, à un signe près je pense.

Ou bien montrer que |AC| = |AB|

:zen:

à un signe près je ne comprend pas?!

[Carpate]

Je n'utilise jamais la méthode par identification, inutilement longue, mais qui aide actuellement où on préfère enseigner des routines que privilégier le raisonnement.
J'avais lu ton calcul en diagonale et cru que tu avais utilisé la méthode par identification ...
Soit j'utilise la méthode de mon message précédent, imbattable en vitesse d'exécution, soit j'utilise la division de 2 polynomes (fussent-ils à coefficients complexes) comme on l'enseignait jadis et c'est tout aussi immédiat.

:zen:

Mais avoue que la méthode par le produit des racines est encore plus rapide ...
Je croyais que la division euclidienne n'était pas au programme. Tu n'es donc pas en terminale ?

[Black Jack]

Mais avoue que la méthode par le produit des racines est encore plus rapide ...
Je croyais que la division euclidienne n'était pas au programme. Tu n'es donc pas en terminale ?

J'étais en Terminale (ou du moins son équivalent) il y a 44 ans ... et pas en France.
Et mon cursus ne s'est pas du tout arreté là. :ptdr:

Mais ce n'est évidemment pas moi qui ai posé les questions initiales.

:zen:

[kapelaony]

je vous remercie de votre aide! cela à été un peu difficile pour moi! merci!

[Carpate]

J'étais en Terminale (ou du moins son équivalent) il y a 44 ans ... et pas en France.
Et mon cursus ne s'est pas du tout arreté là. :ptdr:

Mais ce n'est évidemment pas moi qui ai posé les questions initiales.

:zen:

Et moi il y a 54 ans (1957) !
Mais où sont les neiges d'antant !

Avec ces messages sur une deuxième page j'avais pas fait attention que ce n'était plus kapelaony qui répondait !

[Carpate]

je vous remercie de votre aide! cela à été un peu difficile pour moi! merci!

Bonne continuation.
Tu m'as l'air d'être souvent sur Internet. Tu prépares ton bac à la maison ?

[kapelaony]

Bonne continuation.
Tu m'as l'air d'être souvent sur Internet. Tu prépares ton bac à la maison ?

oui en effet je prépare mon bac a la maison faute de moyen financier! et je ne suis sur internet que seulement lorsque j'ai besoin d'aide pour certaines choses et sur des sites comme celui là qui me semble être un site très fiable!

[Carpate]

oui en effet je prépare mon bac a la maison faute de moyen financier! et je ne suis sur internet que seulement lorsque j'ai besoin d'aide pour certaines choses et sur des sites comme celui là qui me semble être un site très fiable!

Bon courage et peut-être à une autre fois.

[kapelaony]

Bon courage et peut-être à une autre fois.

surement merci j'espère que vous verrez mes demandes!