Les mystères de la fonction exponentielle

[MurphyCooper]

Bonjour, je suis en terminale S et une question hante mes jours et mes nuits depuis déjà plusieurs semaines, enfin, plusieurs questions.
Comme vous avez pu le comprendre dans le titre, il s'agit de la fonction exponentielle. Tout a commencé le jour où l'on a étudié la fonction exponentielle en cours de maths. Les 2 définitions que le prof nous a fait de cette fonction sont les suivantes :

Première : c'est la fonction réciproque de la fonction logarithme népérien, leurs courbes sont symétriques par rapport à la droite d'équation x=y.

Deuxième : C'est la seule et l'unique fonction qui respecte les 4 propriétés suivantes :
-f(0) = 1
-f'(x)=f(x)
-Df=R
-f(x) > 0 pour tout x

Or, je me suis vite rendu compte que l'on utilisait comme notation pour la fonction exponentielle : e^x
Je me suis alors dis : "Mais quel est ce nombre e?", je l'ai tapé sur ma calculatrice et celle-ci a pu m'informer que le nombre e correspondait à un nombre infini qui commençait par : 2,718281....... Puis l'on a commencé à étudier toutes les propriétés telles que : "e^(x+y) = e^x * e^y" ; "e^x - e^y = (e^x)/(e^y)" ; "1/(e^-x) = e^x" , et on les a démontré...
Mais, pourquoi donc le professeur nous donnait-il ces propriétés en nous disant de les apprendre par coeur alors qu'elles sont les mêmes pour tous les nombres puissance x?! Pour moi, e était un nombre comme tout les autres qu'on met puissance x, et que l'on note e car on ne peut pas l'écrire vu que c'est un nombre infini (tout comme π)... Il était alors évident que e^0 était égal à 1 car tout réel puissance 0 est égal à 1... Le nombre e possédait juste la propriété particulière : exp'(x) = exp(x), ce qui était tout à fait normal puisque si f(x) = k^x ; f'(x) = k^(x) * ln(k) ; et ln(e) = 1.
Pour moi, la nouvelle définition de la fonction exponentielle était : "C'est le nombre e puissance x" ; et sa propriété unique était que le nombre e était tel que ln (e) = 1.

Lorsque l'on a démontré les propriétés de la fonction exp valables pour tous les nombres puissance x, ça a été plus fort que moi, j'ai été obligé de faire la remarque au prof. Je m'attendais alors à ce qu'il me donne une explication convaincante, ou qu'il confirme ma remarque et dise que le programme était fait ainsi et que l'on était donc obligé de le suivre. Mais non, il m'a dit : "Le nombre e est en effet égal à 2,718 et des bananes, mais ce n'est qu'une notation et on ne peut pas réduire la fonction exponentielle à cela." Ce que je n'ai absolument pas compris.... Et quand je lui ai demandé pourquoi on démontrait des propriétés valables pour tous les nombres, il m'a dit "En quatrième, vous avez en effet déjà démontré ces propriétés pour n'importe quel nombre a réel. Mais vous ne les avez démontré que pour a^n ; n étant un entier. On le démontre là avec n'importe quels réels x et y." Ce qui ne m'a absolument pas convaincu, car cela fonctionne aussi avec un réel... Mais effectivement, on le démontre en terminale avec la fonction exponentielle car on s'aide de la propriété exp'(x) = exp(x). Et on le démontre en quatrième avec un entier car on s'aide des suites. Mais pourquoi démontre-t-on ces propriétés de cette manière, uniquement avec le nombre e, au lieu de le démontrer avec tous les réels?. J'ai alors cherché sur internet des démonstrations pour ces propriétés, je n'ai malheureusement rien trouvé de satisfaisant, ou alors peut-être était-ce trop compliqué pour moi. Enfin, je pense que l'on nous apprend ces propriétés avec exponentielle comme ceci car sinon ce serait trop compliqué... Mais il existe forcément des démonstration qui prouvent que k^(x+y) = k^x * k^y avec k; x; et y des réels... Mais alors, pourquoi nous apprendre la fonction exponentielle de cette manière? Cela cause d'ailleurs de gros problèmes de compréhension à certains élèves car c'est une manière très abstraite d'aborder la fonction exponentielle...

Merci de bien vouloir m'aider à résoudre ce casse tête :
Pourquoi aborde-t-on la fonction exponentielle de cette manière?
Pourquoi ne démontre-t-on pas que k^(x+y) = k^x * k^y avec k ; x ; et y des réels, ainsi que les autres propriétés?
Pourquoi n'étudions nous même pas les dérivées des fonctions puissance x?

En fait la question principale, c'est Pourquoi étudions nous la fonction exponentielle avant toutes les autres fonctions puissance x? Car cela rend le chapitre totalement abstrait et très mystérieux. On nous apprend des choses, sans nous expliquer le fond en fait... Je trouve ça vraiment étrange...

[zygomatique]

salut

il semble y avoir quelques confusions dans ce que tu dis ...

e est un nombre irrationnel (et même transcendant) comme

exp est le nom d'une fonction comme l'est ln ou cos ... et c'est la fonction définie sur R par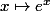

elle prolonge et définit proprement les règles sur les exposants entiers que tu as vu en collège ... mais avec certaines restrictions ...
ainsi essaye de calculer pour voir .... et la justification vient (entre autre) de ce qu'elle est la réciproque de la fonction ln

maintenant pourquoi c'est ce nombre e:

1/ d'abord pour tous réels strictement positifs a et b toute fonction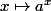 s'exprime en fonction de la fonction 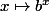et réciproquement ....

2/ ensuite il a fallu choisir un réel de base et pour des raisons de cohérence il a fallu choisir l'unique antécédent de 1 par la fonction ln et on l'a appelé e ....

[MurphyCooper]

Salut, merci pour ta réponse zigomatique, je comprend mieux, en fait, on utilise la fonction exponentielle car sinon on ne pourrait pas utiliser la fonction réciproque ln et du coup il faudrait apprendre plein de choses en plus pour étudier les fonctions c'est ça? En gros c'est une sorte d'approche de choses plus complexes qu'on verra dans le supérieur?

Par contre je n'ai pas trop compris ton 1/ avec la fonction a^x et la fonction b^x...

[Pseuda]

Sais-tu ce que veut dire ou 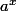? J'imagine que non, parce qu'on ne vous a pas prouvé au lycée l'existence de la fonction (mais uniquement son unicité), et encore moins celle de 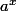, et vous ne savez pas d'où elle sort.

On peut introduire la fonction de plein de manières différentes, mais celle que je trouve la plus "naturelle" (celle d'il y a une dizaine d'années en TeS), c'est celle de dire que c'est la fonction réciproque de la fonction logarithme népérien (lnx), qui elle-même est définie comme l'unique primitive de la fonction qui s'annule en 1 (encore faut-il savoir ce qu'est une primitive, il faut commencer par là dans le programme de TeS, et pourquoi il y en a une seule parmi toutes les primitives d'une fonction qui s'annule en un point donné).

De là, on démontre toutes ses propriétés : transformation d'une somme en un produit, limites, ..., et notamment que la fonction exponentielle est égale à sa dérivée.

Que sont les autres fonctions exponentielles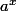 , avec a>0 ? Eh bien, on les définit à leur tour comme les fonctions : 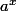= , a>0. Ces fonctions ont toutes les caractéristiques des fonctions exponentielles (transformation d'une somme en un produit...), mais leur dérivée n'est pas égale à elle-même, elle est égale à : .

La fonction est la seule fonction (parmi les fonctions exponentielles, mais aussi parmi toutes les fonctions réelles) dont la dérivée est égale à elle-même. D'où son statut privilégié dans les études de fonctions au lycée, et pour d'autres développements par la suite.

On démontre aussi que ce nombre e est très spécial : il est limite de la suite : quand n tend vers +oo, ou de la somme de la suite 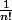(en partant de n=0) quand n tend vers +oo, ...

Il paraît clair aussi que les fonctions exponentielles (puisqu'elles transforment des sommes en produits), sont des prolongements des suites géométriques de 1er terme 1 et de raison q (définies sur N).

En résumé, tes interrogations me semblent tout à fait légitimes.

[MurphyCooper]

C'est bon j'ai compris!!! Merci pseuda! En fait, la fonction exponentielle sert de base à toutes les autres fonctions exponentielles a^x c'est ça?

Parce que si on suit la formule a^x = e^(xlna) ; alors on peut se servir de la fonction exponentielle et de ses propriétés que l'on a démontré grâce à sa dérivée pour démontrer les même propriétés avec toutes les fonction exponentielles a^x!!! Il suffit de faire :

On sait que a^x = e^(xlna) et que e^y * e^x = e^(x+y)

Donc : e^(xlna) * e^(ylna) = e^(xlna + ylna)
= e^((x+y)lna)
=a^(x+y)

DONC a^y * a^x = a^(x+y) !!!!!

[MurphyCooper]

Donc la fonction exponentielle est en fait une base qui est très utile car sa dérivée est égale à elle-même, ce qui nous permet de démontrer plein de choses et de faire des chaînes de démonstrations! Et elle est aussi utile car c'est la fonction réciproque de ln!

J'ai compris?

[Pseuda]

C'est tout à fait ça, tu as tout à fait compris !

[zygomatique]

-f(0) = 1
-f'(x)=f(x)
-Df=R
-f(x) > 0 pour tout x

une remarque en changeant la condition f'(x) = f(x)par f'(x) = kf(x)

tu remarques d'après ce qui précède que la solution est la fonction x --> exp(cx) pour un certain réel c

mais celui ci est l'image d'un certain réel a > 0 par la fonction ln (car l'image de ln est R tout entier)

donc une solution est la fonction x--> exp[x(ln a)] = a^x et on retrouves toutes les fonctions puissances ...