LES MODULOS 2PI : BIZARRE !
52 messages
- Page 2 sur 3 - 1, 2, 3
Re: LES MODULOS 2PI : BIZARRE !
En effet, cela ne va pas (c'est justement le cas que l'on cherche à exclure). Mais cela doit pouvoir se prouver d'une manière ou d'une autre, puisque cela se voit sur la figure.
D'un point intérieur au triangle, si le triangle ABC est direct, on passe de A à B, de B à C, de C à A en tournant dans le sens direct.
A->B->C->A->B. Donc les angles (AB, AC), (BC,BA), (CA,CB) inférieurs à pi, sont orientés dans le même sens.
D'un point intérieur au triangle, si le triangle ABC est direct, on passe de A à B, de B à C, de C à A en tournant dans le sens direct.
A->B->C->A->B. Donc les angles (AB, AC), (BC,BA), (CA,CB) inférieurs à pi, sont orientés dans le même sens.
Re: LES MODULOS 2PI : BIZARRE !
@Pseuda (par rapport à ta dernière remarque d'un point intérieur): je me demande s'il existe une adaptation du théorème de Ceva avec les angles orientés (comme pour le mesures algébriques)... car la forme trigonométrique de ce théorème (https://fr.wikipedia.org/wiki/Th%C3%A9o ... 3.A9trique) permet d'écrire un produit des sinus des angles du triangle = (+-1)... peut-être que ça permet de trouver quelque chose sur les signes de tous les angles.
Je sais pas si cela est à coté du pb, mais pour moi, si on impose un point I à l'intérieur d'un triangle ABC et qu'on mène (AI) et (BI) et (CI), alors on forcément ces droites vont couper les 3 cotés du triangle et pour moi, cela veut dire que si on suppose que (CI) ne coupe pas [AB] mais coupe (AB) (en dehors du triangle) cela contredit le théorème de Ceva...
Donc si on considère M un point particulier intérieur à ABC et qu'on regarde les sinus de tous les angles et qu'on utilise Ceva avec une configuration "5pi/4" cela devrait produire une absurdité (juste une idée brouillon...)
Je sais pas si cela est à coté du pb, mais pour moi, si on impose un point I à l'intérieur d'un triangle ABC et qu'on mène (AI) et (BI) et (CI), alors on forcément ces droites vont couper les 3 cotés du triangle et pour moi, cela veut dire que si on suppose que (CI) ne coupe pas [AB] mais coupe (AB) (en dehors du triangle) cela contredit le théorème de Ceva...
Donc si on considère M un point particulier intérieur à ABC et qu'on regarde les sinus de tous les angles et qu'on utilise Ceva avec une configuration "5pi/4" cela devrait produire une absurdité (juste une idée brouillon...)
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: LES MODULOS 2PI : BIZARRE !
Merci Lostounet, mais j'ai une autre idée toute bête. Si l'un des angles est compris entre 0 et pi, et les 2 autres entre -pi et 0 (par exemple pi/2, -3pi/4 et -3pi/4), pour que la somme des 3 fasse -pi, il faut que les 2 derniers aient une mesure dont la somme soit inférieure à -pi, et géométriquement ça ne passe pas.
Re: LES MODULOS 2PI : BIZARRE !
Ben justement, ce "géométriquement ça passe pas"... ça passe ou ça passe pas ? Mdr
Pour mon exemple avec les (AI) (BI) (CI) on voit clairement que (CI) géométriquement et sans l'ombre d'un doute va couper [AB] mais ce théorème fournit une relation métrique et algèbrique pour le vérifier...
Car si on peut/ veut simplement observer géométriquement, cela est assez clair sur le dessin de base non? Ou alors j'ai mal compris.
Pour mon exemple avec les (AI) (BI) (CI) on voit clairement que (CI) géométriquement et sans l'ombre d'un doute va couper [AB] mais ce théorème fournit une relation métrique et algèbrique pour le vérifier...
Car si on peut/ veut simplement observer géométriquement, cela est assez clair sur le dessin de base non? Ou alors j'ai mal compris.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: LES MODULOS 2PI : BIZARRE !
Je veux dire par là que si la somme de 2 angles d'un triangle est supérieure en valeur absolue à pi, c.a.d 180°, il y a un léger problème.
Je regarderai demain ton théorème de Ceva et la considération sur les droites, qui m'a l'air très intéressante. Je vais me coucher...
Bonne nuit.
Je regarderai demain ton théorème de Ceva et la considération sur les droites, qui m'a l'air très intéressante. Je vais me coucher...
Bonne nuit.
Re: LES MODULOS 2PI : BIZARRE !
A force, je pense avoir une solution rigoureuse (i.e. sans "on le voie sur le dessin).
Si on revient à la définition "archi carré" d'angles où on ne parle pas de mesure des angles mais uniquement en disant qu'un "angle orienté", c'est une rotation vectorielle, c'est à dire une matrice telle que
telle que 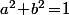 et que "l'angle orienté" entre deux vecteurs unitaires, c'est l'unique rotation qui envoie le premier sur le deuxième.
et que "l'angle orienté" entre deux vecteurs unitaires, c'est l'unique rotation qui envoie le premier sur le deuxième.
Alors dans ce cas, il n'y a plus de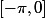 versus
versus 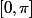 , mais une question de signe de
, mais une question de signe de  (i.e. de signe du sinus) et on vérifie par un simple calcul (*) que dans le cas d'angle entre deux vecteur unitaires, le
(i.e. de signe du sinus) et on vérifie par un simple calcul (*) que dans le cas d'angle entre deux vecteur unitaires, le  c'est le déterminant des deux vecteurs donc que dans le cas de vecteurs pas forcément unitaires le déterminant des deux vecteurs a le même signe que
c'est le déterminant des deux vecteurs donc que dans le cas de vecteurs pas forcément unitaires le déterminant des deux vecteurs a le même signe que  .
.
Enfin, on montre facilement que\!=\!\det\big(\vec{BC},\vec{BA}\big)\!=\!\det\big(\vec{CA},\vec{CB}\big)) et cela prouve que les trois angles d'un triangle ont des
et cela prouve que les trois angles d'un triangle ont des  (i.e. des sinus) de même signe.
(i.e. des sinus) de même signe.
(*)\!=\!b) a le même signe que
a le même signe que  et est égal à
et est égal à  lorsque
lorsque  .
.
Si on revient à la définition "archi carré" d'angles où on ne parle pas de mesure des angles mais uniquement en disant qu'un "angle orienté", c'est une rotation vectorielle, c'est à dire une matrice
Alors dans ce cas, il n'y a plus de
Enfin, on montre facilement que
(*)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: LES MODULOS 2PI : BIZARRE !
Bonjour,
Ok. En effet, l'orientation des angles (compris entre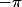 et 0 ou entre 0 et
et 0 ou entre 0 et  ) est donné par le signe du déterminant du couple de vecteurs, et les déterminants des 3 angles considérés sont de même signe.
) est donné par le signe du déterminant du couple de vecteurs, et les déterminants des 3 angles considérés sont de même signe.
Pour une démonstration rigoureuse niveau lycée, je détaille la démonstration ébauchée plus haut.
1) Pour simplifier l'écriture, posons, \beta=(\vec{BC},\vec{BA}), \gamma=(\vec{CA},\vec{CB})) . On vérifie facilement par le calcul que
. On vérifie facilement par le calcul que ) .
.
Ces 3 angles appartiennent chacun, soit à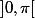 , soit à
, soit à 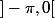 ,
, ) .
.
2) Montrons qu'ils appartiennent tous soit à l'un soit à l'autre de ces 2 intervalles, c.a.d. qu'il ne peut pas y avoir l'un des angles dans un intervalle et les 2 autres dans l'autre.
Pour cela, supposons par exemple que et que
et que  .
.
Comme) , et que
, et que ) , alors
, alors ) , donc
, donc )
3) Comme) alors pour avoir
alors pour avoir ) , c.a.d.
, c.a.d. ) , il faut que l'un ou l'autre appartienne à
, il faut que l'un ou l'autre appartienne à ) et la somme des 2 à
et la somme des 2 à ) . Ceci est impossible concernant les angles d'un triangle (car dans ce cas, l'un des angles est supérieur à un angle droit, et la somme des 2 à un angle plat).
. Ceci est impossible concernant les angles d'un triangle (car dans ce cas, l'un des angles est supérieur à un angle droit, et la somme des 2 à un angle plat).
4) Pour la même raison, on ne peut pas avoir l'un des angles dans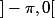 et les 2 autres dans
et les 2 autres dans 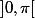 .
.
Ok. En effet, l'orientation des angles (compris entre
Pour une démonstration rigoureuse niveau lycée, je détaille la démonstration ébauchée plus haut.
1) Pour simplifier l'écriture, posons
Ces 3 angles appartiennent chacun, soit à
2) Montrons qu'ils appartiennent tous soit à l'un soit à l'autre de ces 2 intervalles, c.a.d. qu'il ne peut pas y avoir l'un des angles dans un intervalle et les 2 autres dans l'autre.
Pour cela, supposons par exemple que
Comme
3) Comme
4) Pour la même raison, on ne peut pas avoir l'un des angles dans
Re: LES MODULOS 2PI : BIZARRE !
@Lostounet
A partir du moment où l'on a établi que : 3 angles orientés dans le même sens = 3 déterminants de même signe = 3 sinus de même signe = 3 angles compris soit entre 0 et pi soit entre -pi et 0, du coup on n'est plus obligé d'aller chercher un théorème de géométrie faisant appel aux sinus.
Dès lors pour moi, les démonstrations précédentes me paraissent répondre au problème.
Merci Lostounet.
A partir du moment où l'on a établi que : 3 angles orientés dans le même sens = 3 déterminants de même signe = 3 sinus de même signe = 3 angles compris soit entre 0 et pi soit entre -pi et 0, du coup on n'est plus obligé d'aller chercher un théorème de géométrie faisant appel aux sinus.
Dès lors pour moi, les démonstrations précédentes me paraissent répondre au problème.
Merci Lostounet.
Re: LES MODULOS 2PI : BIZARRE !
Pseuda a écrit:
Dès lors pour moi, les démonstrations précédentes me paraissent répondre au problème.
Merci Lostounet.
Effectivement,
Mais je réfléchis toujours à la possibilité d'adapter ce "produit des sinus" au problème posé.
En tout cas, bravo à vous d'avoir trouvé un moyen simple de répondre au problème (je refais votre preuve au brouillon pour voir).
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: LES MODULOS 2PI : BIZARRE !
Je comprend pas : le bleu je suis d'accord (encore que je vois pas l'intérêt de faire intervenir à certains endroits du ]0,pi[ puis juste après du ]-2pi,-pi[ vu que c'est exactement la même chose.Pseuda a écrit:3) Commealors pour avoir
, c.a.d.
, il faut que l'un ou l'autre appartienne à
et la somme des 2 à
. Ceci est impossible concernant les angles d'un triangle (car dans ce cas, l'un des angles est supérieur à un angle droit, et la somme des 2 à un angle plat).
Par contre je vois pas pourquoi "c'est impossible" : comment démontre tu, sans dire que "ça se voit sur un dessin" qu'il est impossible d'avoir un angle plus grand qu'un angle droit (et en plus il faudrait préciser ce que ça signifie) et que la somme des deux autre est supérieure à un angle plat (même remarque) ?
Ca donne fortement l'impression d'un "mordage de queue", non ?
Pour revenir à du complètement "terre à terre", si on prend les angles pi/2 , 5pi/4 et 5pi/4 (de somme pi [2pi]) correspondant au premier problème de nanneb, comment montre tu qu'un tel triangle n'existe pas ?
Tu peut bien sur me répondre "parce que les deux angles de 5pi/4 ont une somme qui est absurde" (ou je sais pas quelle autre somme de deux angles), mais j'aimerais que tu m'explique pourquoi cette somme est absurde.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: LES MODULOS 2PI : BIZARRE !
Bonjour,
C'est curieux comme je m'étais déjà posé la question :
lycee/sens-direct-triangle-t166013.html
En effet, complétons. Les angles et
et  étant tous deux indirects, donc tournant à moins de
étant tous deux indirects, donc tournant à moins de  dans le même sens, leurs valeurs algébriques, et donc géométriques, s'ajoutent pour être comprises entre
dans le même sens, leurs valeurs algébriques, et donc géométriques, s'ajoutent pour être comprises entre  et
et  , donc la somme des angles géométriques leur correspondant, dépasse l'angle plat.
, donc la somme des angles géométriques leur correspondant, dépasse l'angle plat.
Par ailleurs, je ne veux pas m'embêter avec le cas limite (qui n'en est pas un) du triangle aplati. C'est pourquoi je considère que toutes les bornes sont ouvertes.
Alors là ce n'est pas difficile. Un angle orienté de 5pi/4 correspond à un angle géométrique de 3pi/4 (angle saillant) ou de 5pi/4 (angle rentrant). Un angle géométrique de 5pi/4 dans un triangle paraît difficilement concevable, tout comme 2 angles de chacun 3pi/4, dont la somme fait 3pi/2.
J'avoue que cette démonstration me satisfait moyennement. J'ai essayé avec le théorème de l'angle inscrit et les angles au centre qui tournent dans le même sens et dont la somme fait le tour complet. Tu en as peut-être une autre (niveau lycée, c.a.d. qui n'utilise pas les signes des déterminants, les transformations,... ) ? Cela m'intéresse.
C'est curieux comme je m'étais déjà posé la question :
lycee/sens-direct-triangle-t166013.html
Ben314 a écrit:Ceci est impossible concernant les angles d'un triangle (car dans ce cas, l'un des angles est supérieur à un angle droit, et la somme des 2 à un angle plat).Je comprend pas : le bleu je suis d'accord (encore que je vois pas l'intérêt de faire intervenir à certains endroits du ]0,pi[ puis juste après du ]-2pi,-pi[ vu que c'est exactement la même chose.
Par contre je vois pas pourquoi "c'est impossible" : comment démontre tu, sans dire que "ça se voit sur un dessin" qu'il est impossible d'avoir un angle plus grand qu'un angle droit (et en plus il faudrait préciser ce que ça signifie) et que la somme des deux autre est supérieure à un angle plat (même remarque) ?
Ca donne fortement l'impression d'un "mordage de queue", non ?
En effet, complétons. Les angles
Par ailleurs, je ne veux pas m'embêter avec le cas limite (qui n'en est pas un) du triangle aplati. C'est pourquoi je considère que toutes les bornes sont ouvertes.
Ben314 a écrit:Pour revenir à du complètement "terre à terre", si on prend les angles pi/2 , 5pi/4 et 5pi/4 (de somme pi [2pi]) correspondant au premier problème de nanneb, comment montre tu qu'un tel triangle n'existe pas ?
Tu peut bien sur me répondre "parce que les deux angles de 5pi/4 ont une somme qui est absurde" (ou je sais pas quelle autre somme de deux angles), mais j'aimerais que tu m'explique pourquoi cette somme est absurde.
Alors là ce n'est pas difficile. Un angle orienté de 5pi/4 correspond à un angle géométrique de 3pi/4 (angle saillant) ou de 5pi/4 (angle rentrant). Un angle géométrique de 5pi/4 dans un triangle paraît difficilement concevable, tout comme 2 angles de chacun 3pi/4, dont la somme fait 3pi/2.
J'avoue que cette démonstration me satisfait moyennement. J'ai essayé avec le théorème de l'angle inscrit et les angles au centre qui tournent dans le même sens et dont la somme fait le tour complet. Tu en as peut-être une autre (niveau lycée, c.a.d. qui n'utilise pas les signes des déterminants, les transformations,... ) ? Cela m'intéresse.
Re: LES MODULOS 2PI : BIZARRE !
Je t'avoue que moi aussi ça me "satisfait pas trop", mais que je pense pas qu'il y ait moyen de faire autrement au niveau Lycée (sans parler du fait qu'à mon avis, au Lycée, le mieux, c'est de se contenter d'un "ça se voit sur un dessin" plutôt que de "pinailler" à chercher une preuve formelle).Pseuda a écrit:J'avoue que cette démonstration me satisfait moyennement. J'ai essayé avec le théorème de l'angle inscrit et les angles au centre qui tournent dans le même sens et dont la somme fait le tour complet. Tu en as peut-être une autre (niveau lycée, c.a.d. qui n'utilise pas les signes des déterminants, les transformations,... ) ? Cela m'intéresse.
Et le coté "pas trop satisfaisant", il me semble assez évident : tout ce qui est "angle non orienté", c'est vu au collège avec évidement aucune définition formelle permettant de démontrer les truc évidents "qu'on voit sur le dessin" donc de se baser là dessus pour faire une preuve formelle, c'est évidement pas terrible.
Et si on cherche à formaliser correctement cette notion "d'angle géométrique" (=non orienté), c'est passablement la merde et en plus, y'a plus de structure algébrique dessus (quand tu "somme" deux angles non orientés
Bref, pour répondre à ta question "comment faire super propre sans les déterminants ou autres truc non vus au Lycée", ben j'ai pas de réponse, et je pense assez fort qu'il n'y en a pas.
A la limite, on peut se demander comment faire "le moins crado possible" ou plutôt "le plus convainquant possible pour un éventuel (*) Lycéen qui se poserait la question", et là, il me semble que de revenir aux angles géométrique du collège, c'est peut-être ce qu'on peut faire de mieux.
(*) Ça doit pas courir les rues...
P.S. Sinon, effectivement, les cas particulier avec des angles plats, c'est pas ça le problème et c'est pour ça que je te demandais juste une réponse face à un cas particulier style pi/2 , 5pi/4, 5pi/4 qui suffit amplement à voir le problème et qui évite les "préliminaires" du style "si un des 3 angles est comme çi alors il y en a forcément un des autres comme ça . . ."
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: LES MODULOS 2PI : BIZARRE !
Les angles géométriques (non orientés) ne me paraissent pas moins "valables" que les angles orientés.
Par exemple un angle orienté confond 5pi/4 et -3pi/4 tandis qu'un angle géométrique distingue bien les 2 (angle saillant et angle rentrant). Les angles orientés m'apparaissent plus être un endroit d'"atterrissage" sur le cercle orienté.
Bref, pour en revenir aux démonstrations, je pense aussi qu'il faut, à moment donné, en revenir aux angles géométriques, et qu'on ne peut pas y arriver par le calcul avec les angles orientés.
Du coup ma démo me paraît quand même valable. Mais je suis d'accord pour dire que, quitte à en revenir aux angles géométriques, autant utiliser le théorème de l'angle inscrit et dire :
Pour que les 3 angles orientés au centre du cercle circonscrit au triangle, doubles des angles orientés du triangle, fassent un tour complet, il faut que ces 3 angles soient orientés dans le même sens, donc que les angles du triangle le soient aussi (puisque l'angle inscrit est orienté dans le même sens que son angle au centre). Ouf.
Par exemple un angle orienté confond 5pi/4 et -3pi/4 tandis qu'un angle géométrique distingue bien les 2 (angle saillant et angle rentrant). Les angles orientés m'apparaissent plus être un endroit d'"atterrissage" sur le cercle orienté.
Bref, pour en revenir aux démonstrations, je pense aussi qu'il faut, à moment donné, en revenir aux angles géométriques, et qu'on ne peut pas y arriver par le calcul avec les angles orientés.
Du coup ma démo me paraît quand même valable. Mais je suis d'accord pour dire que, quitte à en revenir aux angles géométriques, autant utiliser le théorème de l'angle inscrit et dire :
Pour que les 3 angles orientés au centre du cercle circonscrit au triangle, doubles des angles orientés du triangle, fassent un tour complet, il faut que ces 3 angles soient orientés dans le même sens, donc que les angles du triangle le soient aussi (puisque l'angle inscrit est orienté dans le même sens que son angle au centre). Ouf.
Re: LES MODULOS 2PI : BIZARRE !
Oui, mais là, quand tu écrit que "... confond 5pi/4 et -3pi/4", c'est pas d'angles que tu parle, mais de mesure d'angles, ce qui déjà est infiniment plus compliqué à définir proprement que la notion d'angle et qui, effectivement traduit "assez mal" la notion d'angle les "angles orientés", c'est clairement le groupe R/(2pi.Z) qui les représente et de regarder le truc dans R, c'est forcément la merde à cause du quotient qu'on a pas fait.
Un "angle", LA seule et unique définition valable (en tout cas permettant de tout démontrer très rapidement et de façon on ne plus formelle), c'est un élément de SO(R^2), c'est à dire une rotation vectorielle.
Et du fait que, muni de la loi de composition SO(R^2) est non seulement un groupe, mais même un groupe commutatif, on se permet (comme c'est l'usage dans le cas commutatif) de noter + la loi.
SO(R^2) est non seulement un groupe, mais même un groupe commutatif, on se permet (comme c'est l'usage dans le cas commutatif) de noter + la loi.
Ensuite, l'autre truc "magique" de SO(R^2), c'est qu'il agit "simplement transitivement" sur les couples de vecteurs unitaires, c'est à dire que, étént donné deux vecteurs unitaires X et X' il existe un unique élément de SO(R^2) (i.e. une unique rotation, i.e. un unique "angle") qui envoie X sur X' et c'est cet élément de SO(R^2) qui s'appelle "l'angle (orienté) entre X et X'".
Bref, de la même façon que les "vecteur" correspondent directement à l'action des translations sur les points, les "angles orientés" correspondent directement à l'action des rotations vectorielles sur les vecteurs unitaires (et la construction est d'ailleurs exactement la même : Le groupe des translations est un groupe commutatif qui agit simplement transitivement sur les couples de points : si A,B sont deux points fixés, il y a une unique translation telle que A->B)
Et maintenant que j'ai rappelé quel est la définition on ne peut plus rigoureuse de ce qu'est "un angle orienté" (et pas de ce qu'est la mesure d'un tel angle), a toi de jouer pour voir ce que tu propose comme définition rigoureuse de ce qu'est "un angle géométrique".
P.S. Et à mon avis, ton coups "des angles aux centres du cercle circonscrit", je pense que ça continue à "se mordre la queue" vu que le fait que "3 angles soient orientés dans le même sens", je vois pas trop d'où tu le sort (à part de la figure).
Un "angle", LA seule et unique définition valable (en tout cas permettant de tout démontrer très rapidement et de façon on ne plus formelle), c'est un élément de SO(R^2), c'est à dire une rotation vectorielle.
Et du fait que, muni de la loi de composition
Ensuite, l'autre truc "magique" de SO(R^2), c'est qu'il agit "simplement transitivement" sur les couples de vecteurs unitaires, c'est à dire que, étént donné deux vecteurs unitaires X et X' il existe un unique élément de SO(R^2) (i.e. une unique rotation, i.e. un unique "angle") qui envoie X sur X' et c'est cet élément de SO(R^2) qui s'appelle "l'angle (orienté) entre X et X'".
Bref, de la même façon que les "vecteur" correspondent directement à l'action des translations sur les points, les "angles orientés" correspondent directement à l'action des rotations vectorielles sur les vecteurs unitaires (et la construction est d'ailleurs exactement la même : Le groupe des translations est un groupe commutatif qui agit simplement transitivement sur les couples de points : si A,B sont deux points fixés, il y a une unique translation telle que A->B)
Et maintenant que j'ai rappelé quel est la définition on ne peut plus rigoureuse de ce qu'est "un angle orienté" (et pas de ce qu'est la mesure d'un tel angle), a toi de jouer pour voir ce que tu propose comme définition rigoureuse de ce qu'est "un angle géométrique".
P.S. Et à mon avis, ton coups "des angles aux centres du cercle circonscrit", je pense que ça continue à "se mordre la queue" vu que le fait que "3 angles soient orientés dans le même sens", je vois pas trop d'où tu le sort (à part de la figure).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: LES MODULOS 2PI : BIZARRE !
Bonjour,
Tu verras dans n'importe quel livre du collège (et même du primaire je crois) la définition de l'angle (géométrique) : "Un angle est formé de deux demi-droites de même origine. Cette origine est appelé le sommet de l'angle. Les demi-droites sont appelés les côtés de l'angle :
http://www.mathox.net/cinquiemes_angles.html
A mon tour, peux-tu m'expliquer pourquoi les démonstrations basées sur la considération d'angles géométriques (celles vues au collège jusqu'en 2nde) se mordent la queue ?
Pour moi, dès que les angles orientés et
et sont de sens différents, l'un est direct, l'autre indirect, leurs mesures d'angles géométriques se soustraient au lieu de s'additionner. En clair, elles sont basées sur :
sont de sens différents, l'un est direct, l'autre indirect, leurs mesures d'angles géométriques se soustraient au lieu de s'additionner. En clair, elles sont basées sur :
si \in ]0,\pi[) , et
, et  \in ]-\pi, 0[) , alors
, alors 
et si) , et
, et ) , tous deux
, tous deux  ou tous deux dans
ou tous deux dans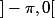 , alors
, alors 
On a exactement la même chose pour les mesures algébriques des longueurs (longueurs affectées d'un signe, disparues des programmes du secondaire) :
si A, B et C sont 3 points alignés dans cet ordre : AC = AB + BC
si A, B et C sont 3 points alignés dans un ordre différent : AC = |AB - BC|
Tu verras dans n'importe quel livre du collège (et même du primaire je crois) la définition de l'angle (géométrique) : "Un angle est formé de deux demi-droites de même origine. Cette origine est appelé le sommet de l'angle. Les demi-droites sont appelés les côtés de l'angle :
http://www.mathox.net/cinquiemes_angles.html
A mon tour, peux-tu m'expliquer pourquoi les démonstrations basées sur la considération d'angles géométriques (celles vues au collège jusqu'en 2nde) se mordent la queue ?
Pour moi, dès que les angles orientés
si
et si
On a exactement la même chose pour les mesures algébriques des longueurs (longueurs affectées d'un signe, disparues des programmes du secondaire) :
si A, B et C sont 3 points alignés dans cet ordre : AC = AB + BC
si A, B et C sont 3 points alignés dans un ordre différent : AC = |AB - BC|
Re: LES MODULOS 2PI : BIZARRE !
Tout simplement parce que cette définition là :
Si un angle c'était "un couple de demi droites", alors ça voudrait évidement dire que, pour que deux angles soient égaux, ben faudrait que ce soit le "même couple de demi droites" et ça colle absolument pas avec la vision "naïve" de ce qu'est un angle (*).
Bref, c'est exactement la même chose que pour les vecteurs : que tu emploie explicitement le mot de "quotient" où pas, tu ne coupera pas au fait qu'il y a des truc au départ différents que tu va te mettre à considérer comme égaux, par exemple que des couples de droites différents vont donner des angles égaux ou que des couples de points différents vont donner des vecteurs égaux.
Et ce type de truc, y'a absolument pas photo, en math., y'a qu'une et une seule façon de le définir proprement, c'est des passages au quotient (ou des action de groupes, ce qui revient fondamentalement au même).
Bref, si effectivement c'est texto ça qu'il y a d'écrit dans les programmes de cinquième sans que soit rajouté un truc du style "qu'on s'autorise à déplacer/retourner le dessin comme s'il était fait sur du papier calque" (= on passe au quotient), c'est totalement délirant vu que ca signifie que, quand on va leur demander ensuite de comprendre la notion, ben ça colle absolument pas avec la soit disant définition qu'on leur a donné (tant qu'à faire, il vaudrait 100 fois mieux ne donner aucune définition plutôt que d'en donner une aussi fausse que ça)
(*) Et d'ailleurs je comprend même pas comment certains (rares) élèves arrivent à finir par comprendre ce qu'est réellement un angle en partant de ça comme définition. Ou plutôt, je devrais dire que je comprend parfaitement : la seule solution pour comprendre cette notion d'angle, ben c'est clairement de complètement oublier la définition débile pour uniquement se baser sur les propriétés comprises au fur et à mesure des exo. sans surtout chercher à faire le moindre lien avec la définition (et pour cause...)
ben elle veut absolument rien dire où, plus précisément, elle ne défini absolument pas ce qu'est un angle.Pseuda a écrit:Un angle est formé de deux demi-droites de même origine. Cette origine est appelé le sommet de l'angle. Les demi-droites sont appelés les côtés de l'angle :
Si un angle c'était "un couple de demi droites", alors ça voudrait évidement dire que, pour que deux angles soient égaux, ben faudrait que ce soit le "même couple de demi droites" et ça colle absolument pas avec la vision "naïve" de ce qu'est un angle (*).
Bref, c'est exactement la même chose que pour les vecteurs : que tu emploie explicitement le mot de "quotient" où pas, tu ne coupera pas au fait qu'il y a des truc au départ différents que tu va te mettre à considérer comme égaux, par exemple que des couples de droites différents vont donner des angles égaux ou que des couples de points différents vont donner des vecteurs égaux.
Et ce type de truc, y'a absolument pas photo, en math., y'a qu'une et une seule façon de le définir proprement, c'est des passages au quotient (ou des action de groupes, ce qui revient fondamentalement au même).
Bref, si effectivement c'est texto ça qu'il y a d'écrit dans les programmes de cinquième sans que soit rajouté un truc du style "qu'on s'autorise à déplacer/retourner le dessin comme s'il était fait sur du papier calque" (= on passe au quotient), c'est totalement délirant vu que ca signifie que, quand on va leur demander ensuite de comprendre la notion, ben ça colle absolument pas avec la soit disant définition qu'on leur a donné (tant qu'à faire, il vaudrait 100 fois mieux ne donner aucune définition plutôt que d'en donner une aussi fausse que ça)
(*) Et d'ailleurs je comprend même pas comment certains (rares) élèves arrivent à finir par comprendre ce qu'est réellement un angle en partant de ça comme définition. Ou plutôt, je devrais dire que je comprend parfaitement : la seule solution pour comprendre cette notion d'angle, ben c'est clairement de complètement oublier la définition débile pour uniquement se baser sur les propriétés comprises au fur et à mesure des exo. sans surtout chercher à faire le moindre lien avec la définition (et pour cause...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: LES MODULOS 2PI : BIZARRE !
Et pour en rajouter une couche, là ou tu vois la profonde débilité du système actuel, c'est que si tu donnait comme définition d'un angle que c'est "ce qu'on mesure avec un rapporteur", ben tout le monde serait content : les élèves parce que c'est pas bien méchant comme définition et les "bourbakistes" qui voient immédiatement que le fait qu'on s'autorise à déplacer le rapporteur où on veut sur la feuille, ça signifie très précisément qu'on est en train de faire un passage au quotient : on identifie comme étant égales des choses placés à des endroits différents du dessin. Et je pense que tu sais comme moi que c'est ça qui a du mal à passer auprès des élèves ( que ce soit en ce qui concerne les angles ou les vecteurs) Là, c'est "royal" vu que c'est précisément le fait qu'on peut déplacer le rapporteur qui explique le phénomène.
C'est un peu moins "visuel" concernant les vecteur vu qu'on ne s'autorise plus à faire "tourner" l'appareil qui mesure, mais uniquement à le déplacer (=translater) et c'est moins naturel.
C'est un peu moins "visuel" concernant les vecteur vu qu'on ne s'autorise plus à faire "tourner" l'appareil qui mesure, mais uniquement à le déplacer (=translater) et c'est moins naturel.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: LES MODULOS 2PI : BIZARRE !
Elle se "mordent pas la queue", mais elle reposent forcément sur une définition "qu'on voit sur le dessin" et pas sur quelque chose de formel. Et si ce "on voit sur le dessin" tu veut l'écrire de façon formelle, ben ce qu'il faut faire, c'est quotienter les couples de vecteurs unitaire par tout le groupe O(R^2) de façon à identifier (X,X') avec (X',X) sauf que les deux gros problème, c'est quePseuda a écrit:A mon tour, peux-tu m'expliquer pourquoi les démonstrations basées sur la considération d'angles géométriques (celles vues au collège jusqu'en 2nde) se mordent la queue ?
- Le groupe n'agit plus simplement transitivement sur les couples de vecteurs unitaires (i.e. "un angle" ce n'est plus un élément du groupe en question, mais un quotient de ce groupe)
- Le groupe O(R^2) n'est pas commutatif et en plus, la structure de groupe ne passe pas au quotient permettant de définir les angles donc tu as des angles, certes, mais avec aucune structure algébrique dessus dan ça va pas servir à grand chose.
Bref, c'est bien plus difficile à définir formellement ce qu'est un "angle géométrique" et c'est infiniment moins utile algébriquement parlant. Donc si on parle de faire des preuves formelles et pas axées sur du "on voit sur le dessin que", ça a pas d'intérêt.
Et sinon, dans la suite de ton post, tu mélange une fois de plus la notion d'angle et celle de mesure d'angle. Et je te le (re)dit, la notion de mesure d'angle, si on en veut une vrai définition formelle permettant de faire des preuves carrées, c'est beaucoup beaucoup plus compliqué que la notion d'angles.
Sinon, à mon époque, on faisait encore proprement les mesures algébrique et ce n'était pas du tout "une longueur munie d'un signe".
On partait de la (unique) coordonnée
Et par rapport à la notion de "longueur" (qui n'a de sens que dans le cas où on est sur un plan Euclidien), je ne garde pas de souvenir qu'ont ait jamais privilégié le choisir un vecteur unitaire
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: LES MODULOS 2PI : BIZARRE !
Je suis d'accord qu'avec les angles géométriques, pour faire les calculs, "on marche sur des oeufs", il faut regarder le dessin ... Mais on ne peut pas expliquer à des élèves de 6ème le groupe des rotations, commutatif, qui opère transitivement..., et je t'assure qu'ils comprennent très bien ce qu'est un angle, et qu'ils font eux-mêmes dans leur tête la relation que si 2 angles sont égaux, cela veut dire qu'en fait leur mesure sont égales (sinon quel sens donner à l'angle ABC = l'angle DEF ?). Je suis contre trop de formalisme, mais pour la rigueur.
Par contre, pour les vecteurs, les élèves s'embrouillent au début avec les vecteurs et les vecteurs
et les vecteurs  (mais cela finit par venir), et on se demande si, en voulant simplifier les choses (on ne parle plus de bi-points, de classes d'équivalence, de vecteur libre ou lié, ..., toutes choses très fouillées, mais on parle quand même de direction, sens, longueur, ouf) on ne les a pas finalement un peu embrouillées.
(mais cela finit par venir), et on se demande si, en voulant simplifier les choses (on ne parle plus de bi-points, de classes d'équivalence, de vecteur libre ou lié, ..., toutes choses très fouillées, mais on parle quand même de direction, sens, longueur, ouf) on ne les a pas finalement un peu embrouillées.
Je trouve aussi que la notion de mesure algébrique manque parfois (pour la réciproque du théorème de Thalès, on utilisait cette notion au lieu de "points dans le même ordre"). Dommage.
Bref.
Par contre, pour les vecteurs, les élèves s'embrouillent au début avec les vecteurs
Je trouve aussi que la notion de mesure algébrique manque parfois (pour la réciproque du théorème de Thalès, on utilisait cette notion au lieu de "points dans le même ordre"). Dommage.
Bref.
Re: LES MODULOS 2PI : BIZARRE !
a) Selon toi, est ce que de définir un angle comme "ce qu'on mesure avec un rapporteur" est un "excès de formalisme" ?Pseuda a écrit:...et je t'assure qu'ils comprennent très bien ce qu'est un angle, et qu'ils font eux-mêmes dans leur tête la relation que si 2 angles sont égaux, cela veut dire qu'en fait leur mesure sont égales (sinon quel sens donner à l'angle ABC = l'angle DEF ?). Je suis contre trop de formalisme, mais pour la rigueur.
b) Toujours selon toi, peut tu m'expliquer comment un truc qui est défini comme étant (du verbe être) un couple de demi droites peut être situé à plusieurs endroit sur la figure ?
Donc je persiste et je signe : oui ils finissent par comprendre ce qu'est un angle, mais il faut qu'ils commencent par jeter totalement à la poubelle la définition qu'on leur a donné vu qu'elle colle absolument pas avec ce qu'on leur demande de faire ensuite.
Concrètement parlant, l'élève qui te dit qu'il comprend pas que l'angle ABC c'est le même que DEF vu que c'est pas les même demi droites et que la définition dit qu'un angle c'est un couple de demi droite, tu lui répond quoi ?
Le problème c'est absolument de savoir s'il faut faire du formalisme ou pas : bien sûr que non, le but c'est qu'ils apprennent à manipuler la notion. Donc la définition, c'est pas important, mais de là à écrire en noir su blanc une définition totalement fausse et qui va à l'encontre même de la notion qu'on veut définir, là, y'a pas photo : il vaut 100 fois mieux ne rien écrire du tout !!!!!
Et là où ça me "trou le cul" encore plus, c'est que la notion d'angle située nulle part en particulier sur le dessin, c'est quand même pas compliqué d'en donner une définition très simple et au fond très rigoureuse à coup de papier calque et/ou de rapporteur et/ou en utilisant des truc comme "dessin superposables", etc... : c'est pas le choix qui manque pour donner une très bonne idée CORRECTE de ce que c'est.
P.S.1 : Et le groupe SO(R^2) et les quotients, c'est pour t'explique A TOI (et surement pas aux élève) que tu fera jamais rien de propre avec la notion d'angle géométrique. Idem pour la distinction entre angle et mesure : si tu veut des trucs "propres", ben t'as surtout pas intérêt de "descendre" au niveau de la notion de mesure d'angle.
P.S.2 : Et justement, ça
Tu as pas l'impression que ça serait quand même "un peu mieux" si, plutôt qu'il soit obligés dans leur tête (et à force d'exercices) de finir par comprendre que angle=mesure (ce qui est contradictoire avec la définition donnée) ça serait un tout petit peu plus malin de leur donner une définition correcte ?Pseuda a écrit:...qu'ils font eux-mêmes dans leur tête la relation que si 2 angles sont égaux, cela veut dire qu'en fait leur mesure sont égales (sinon quel sens donner à l'angle ABC = l'angle DEF ?)
Bref, qu'ils aient une définition qui correspond à ce qu'il faut qui comprennent et qui ne dit pas le contraire.
Ou alors, l'autre option, c'est qu'on veuille justement (et à contrario de ce qu'on aimerais qu'il finissent par comprendre) dire que ABC et DEF c'est des angles différents mais qui ont même mesure. Si c'est bien ça alors j'hallucine vu que, y compris avec la définition archi. rigoureuse (action de groupe ou quotients) ce sont bien les même angles et pas des angles différents de même mesure.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
52 messages
- Page 2 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 97 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
