Les Limites - Exercices incompris - Serie ES
Désolé du double post, mais on ne peut pas modifier.
Donc, 2. Identifie alors les coefficients de cette expression avec lexpression de départ. Tu dois obtenir un système de 4 équations. Détermine alors les valeurs des trois coefficients , a, b et c.
Les coefficients sont-ils a=7 b=2 et c =2
Par contre, je n'ai pas compris pourquoi on est censé obtenir un système de 4 équations.
Merci d'avance.
Donc, 2. Identifie alors les coefficients de cette expression avec lexpression de départ. Tu dois obtenir un système de 4 équations. Détermine alors les valeurs des trois coefficients , a, b et c.
Les coefficients sont-ils a=7 b=2 et c =2
Par contre, je n'ai pas compris pourquoi on est censé obtenir un système de 4 équations.
Merci d'avance.
Je nai pas les mêmes résultats. Comment as-tu fait pour les trouver ?
Tu dois procéder ainsi :
1re étape : Je développe puis je réduis lexpression de lénoncé en mettant en facteur chaque terme de même degré avec ses coefficients :
(ax^2+bx+c))
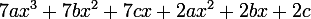
x^2+(7c+2b)x+ 2c)
2e étape : Jidentifie les termes (ou coefficients) à lexpression connue de la fonction donnée (sans coefficients indéterminés) :
Expression connue :
Système déquations didentification :
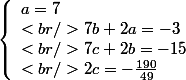
À partir de là, détermine les trois coefficients.
Si tu ne comprends pas quelque chose, nhésite pas à demander.
Tu dois procéder ainsi :
1re étape : Je développe puis je réduis lexpression de lénoncé en mettant en facteur chaque terme de même degré avec ses coefficients :
2e étape : Jidentifie les termes (ou coefficients) à lexpression connue de la fonction donnée (sans coefficients indéterminés) :
Expression connue :
Système déquations didentification :
À partir de là, détermine les trois coefficients.
Si tu ne comprends pas quelque chose, nhésite pas à demander.
Sois plus concentré sur ce que tu fais. Vérifie si cest bien cohérent.Styme a écrit:Merci beaucoup.
Donc, j'ai trouvé :
7a =7 ; a= 1 ==> OK.
7b+2a=-3 ; 7b+a =-3/2 ; 7b+a=-1.5 ; b+a= -1.5/7 ==> Attention ! Quest-ce que tu as fait ici ? Tu ne peux diviser seulement un terme !! Si tu le fais, tu les divises tous..
7c+2b=-15 ; 7c+b=-15/2 ; 7c+b = -7.5 ; cb =-7.5/15 ; cb = -0.5 ==> Même remarque. Recommence en procédant comme je tai montré ci-dessus.
2c = -190/49 ; c = -190/49/2 : environ -1.94 ==> Pas dapproximation dans ce genre de calcul.. Tu gardes cette valeur exacte.
Est-ce bon ?
Merci d'avance.
Attention !Styme a écrit:7a =7 ; a= 1
7c+2b=-15 ; 7c=-15-2b = -15-2 = -17 c = -17/7 ==> Tu ne connais pas encore b. Comment peux-tu le remplacer par 1 ? Tu dois résoudre léquation ci-dessous avant dentamer celle-la (avec la valeur de b).
7b+2a = -3 7b = -3-2a = -3-2 = -5 b=-5/7
2c = -190/49
c = -190/49/2 ==> =-95/49 (réduis la fraction).
Est-ce bon ?
Merci d'avance.
7a =7 ; a= 1
7c+2b=-15 ; 7c=-15-2b = -15-2 = -17 <-> c = -17/7 ==> Tu ne connais pas encore b. Comment peux-tu le remplacer par 1 ? Tu dois résoudre léquation ci-dessous avant dentamer celle-la (avec la valeur de b).
7b+2a = -3 <-> 7b = -3-2a = -3-2 = -5 <-> b=-5/7
7c+2b=-15 ; 7c=-15-2x(-5/7) ; 7c =15 - (-10x/7) ; 7c = 105/7 + 10x/7 ; 7c = 15+10x/7 ; c= 15+10x/7 x 7 ; c = 15+10 = 25
2c = -190/49
c = -190/49/2 ==> =-95/49 = On ne peut pas réduire.
Est-ce bon ?
Merci d'avance.
7c+2b=-15 ; 7c=-15-2b = -15-2 = -17 <-> c = -17/7 ==> Tu ne connais pas encore b. Comment peux-tu le remplacer par 1 ? Tu dois résoudre léquation ci-dessous avant dentamer celle-la (avec la valeur de b).
7b+2a = -3 <-> 7b = -3-2a = -3-2 = -5 <-> b=-5/7
7c+2b=-15 ; 7c=-15-2x(-5/7) ; 7c =15 - (-10x/7) ; 7c = 105/7 + 10x/7 ; 7c = 15+10x/7 ; c= 15+10x/7 x 7 ; c = 15+10 = 25
2c = -190/49
c = -190/49/2 ==> =-95/49 = On ne peut pas réduire.
Est-ce bon ?
Merci d'avance.
Décidément, je ne comprends pas ce que tu fais... :hum:Styme a écrit:7a =7 ; a= 1
7c+2b=-15 ; 7c=-15-2b = -15-2 = -17 c = -17/7 ==> Tu ne connais pas encore b. Comment peux-tu le remplacer par 1 ? Tu dois résoudre léquation ci-dessous avant dentamer celle-la (avec la valeur de b).
7b+2a = -3 7b = -3-2a = -3-2 = -5 b=-5/7
7c+2b=-15 ; 7c=-15-2x(-5/7) ; 7c =-15 - (-10x/7) ; 7c = 105/7 + 10x/7 ; 7c = 15+10x/7 ; c= 15+10x/7 x 7 ; c = 15+10 = 25 ==> Doù vient ce??? Tu avais oublié le « - » devant 15 (ajouté en rouge).
2c = -190/49
c = -190/49/2 ==> =-95/49 = On ne peut pas réduire.
==> Tu dois obtenir les deux mêmes valeurs pour c !! La deuxième est juste.
Est-ce bon ?
Merci d'avance.
On essaie de répondre à cela :
1. Développe (7x+2)(ax^2+bx+c) puis réduis en regroupant tous les coefficients dun terme en \large x de même degré dans une parenthèse.
2. Identifie alors les coefficients de cette expression avec lexpression de départ. Tu dois obtenir un système de 4 équations. Détermine alors les valeurs des trois coefficients \large a, \large b et \large c.
3. Reviens à la forme factorisée donnée dans lénoncé et remplace \large a, \large b et \large c par leurs valeurs respectives, déterminées précédemment.
4. Résous ce produit égal à 0. Tu dois obtenir 3 solutions comme à la question 4.
1. Développe (7x+2)(ax^2+bx+c) puis réduis en regroupant tous les coefficients dun terme en \large x de même degré dans une parenthèse.
2. Identifie alors les coefficients de cette expression avec lexpression de départ. Tu dois obtenir un système de 4 équations. Détermine alors les valeurs des trois coefficients \large a, \large b et \large c.
3. Reviens à la forme factorisée donnée dans lénoncé et remplace \large a, \large b et \large c par leurs valeurs respectives, déterminées précédemment.
4. Résous ce produit égal à 0. Tu dois obtenir 3 solutions comme à la question 4.
Oui.Styme a écrit:Oui, maintenant, il faut déterminer les valeurs de a, b et c, non ?
a et c se déterminent très aisément.
Ensuite, il suffit de reporter leurs valeurs dans une des deux autres pour avoir b.
La dernière équation permet de vérifier les résultats (si elle est vérifiée avec les valeurs déterminées précédemment, cest quelles sont bien justes).
3. Reviens à la forme factorisée donnée dans lénoncé et remplace \large a, \large b et \large c par leurs valeurs respectives, déterminées précédemment.
a = 1
b= -5/7
c= -95/49
(7x+2)(ax²+bx+c)
(7x+2)(1x²+(-5/7x)+(-95/49)
(7x x(1x²))+(7xx-5/7x)+(7xx-95/49)+(2x1x²)+(2x(-5/7x)+(2x(-95/49)
(7x^3)+(35/7x²)+(665x/49)+(2x²)+(-10/7x)+(-190/49)
(7x^3)+(35/7x²+2x²)+(655x/49+-10/7x)+(-190/49)
(7x^3)+(35/7x²+(14/7x²)+(655x/49+(-70/49x)+(-190/49)
(7x^3)+(49/7x²)+(585x/49)+(-190/49)
(7x^3)+(7x²)+(585x/49)+(-190/49)
a = 1
b= -5/7
c= -95/49
(7x+2)(ax²+bx+c)
(7x+2)(1x²+(-5/7x)+(-95/49)
(7x x(1x²))+(7xx-5/7x)+(7xx-95/49)+(2x1x²)+(2x(-5/7x)+(2x(-95/49)
(7x^3)+(35/7x²)+(665x/49)+(2x²)+(-10/7x)+(-190/49)
(7x^3)+(35/7x²+2x²)+(655x/49+-10/7x)+(-190/49)
(7x^3)+(35/7x²+(14/7x²)+(655x/49+(-70/49x)+(-190/49)
(7x^3)+(49/7x²)+(585x/49)+(-190/49)
(7x^3)+(7x²)+(585x/49)+(-190/49)
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 84 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
