Styme a écrit:Oui, merci.
Mais ici, je suis obligé de garder -00 vu qu'on l'a trouvé dans la 1. ==> Non, non et non. On ne lécrit JAMAIS, un point cest tout.
f est continue est strictement croissante sur lintervalle ]-00 ;-5/7[ daprès son tableau des variations. De plus, f(-00) = -00 et f(-5/7) : 135/98 . Comme 0 E [-00 ;135/98], daprès le corollaire du théorème des valeurs intermédiaires, il existe un unique réel a E [-00;135/98] tel que f(a) = 0
f est continue est strictement décroissante sur lintervalle [ -5/7 ;1] daprès son tableau des variations. De plus, f(-5/7) = 135/98 et f(1) : -729/98. Comme 0 E [135/98;-729/98], daprès le corollaire du théorème des valeurs intermédiaires, il existe un unique réel a E [135/98;-729/98] tel que f(a) = 0
Visiblement, tu ne comprends pas ce que je te dis.
Il y a 3 solutions :

est continue est strictement croissante sur lintervalle

daprès son tableau des variations. De plus,
=-\frac{4607}{784}\approx-5,88)
et
=\frac{135}{98}\approx1,38)
. Comme

, daprès le corollaire du théorème des valeurs intermédiaires, il existe un unique réel
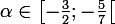
tel que
=0)
.

est continue est strictement décroissante sur lintervalle
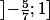
daprès son tableau des variations. De plus,
=\frac{135}{98}\approx1,38)
et
=-\frac{729}{98}\approx-7,44)
. Comme
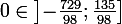
, daprès le corollaire du théorème des valeurs intermédiaires, il existe un unique réel
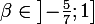
tel que
=0)
.

est continue est strictement croissante de
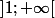
dans
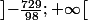
daprès son tableau des variations.
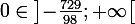
donc, daprès le corollaire du théorème des valeurs intermédiaires, il existe un unique réel
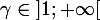
tel que
=0)
.
Jai varié un peu pour la dernière. Les deux commentaires sont tout à fait acceptables et il en existe encore dautres.
