Les limites (1er S)
19 messages
- Page 1 sur 1
les limites (1er S)
malgres quelques reponses je ne vois toujours pas comment faire pour le cas ci present:
étudier les limites de cette fonction en -(infini) en+(infini) et en 0 la fonction est telle que f(x)=x²-x-1+(1/x)
merci pour votre aide
étudier les limites de cette fonction en -(infini) en+(infini) et en 0 la fonction est telle que f(x)=x²-x-1+(1/x)
merci pour votre aide
re,
donc pour les limites en +inf et -inf je vais factoriser par le terme de plus haut degré donc
je commence par la limite en +inf:
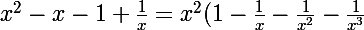)
je pense que ça c'est ok
ensuite tu dois savoir que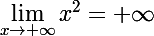 (c'est du cours)
(c'est du cours)
maintenant je vais m'occuper de ce qui est entre parenthese, je vais decomposer en prenant chaque terme qui la compose donc
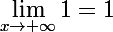
ensuite
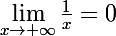 (c'est du cours)
(c'est du cours)
ensuite
 (c'est du cours egalement)
(c'est du cours egalement)
enfin
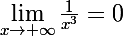 (egalement du cours)
(egalement du cours)
donc
=1)
donc en fait x^2 tend vers +inf quand x->+inf et ce qui est entre parenthese tend vers 1 quand x->+inf (on a quelque chose de la forme )
)
donc
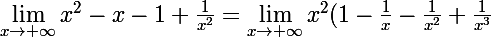=+\infty)
essaie de faire la limite en -inf
désolé mais je ne comprend toujours pas
donc pour les limites en +inf et -inf je vais factoriser par le terme de plus haut degré donc
je commence par la limite en +inf:
je pense que ça c'est ok
ensuite tu dois savoir que
maintenant je vais m'occuper de ce qui est entre parenthese, je vais decomposer en prenant chaque terme qui la compose donc
ensuite
ensuite
enfin
donc
donc en fait x^2 tend vers +inf quand x->+inf et ce qui est entre parenthese tend vers 1 quand x->+inf (on a quelque chose de la forme
donc
essaie de faire la limite en -inf
Allez prends ton cours sur les limites, ça ira mieux ...
Tu l'as ?
Limites des fonctions usuelles :
-Quand x->-inf , x²->+inf (d'accord ? Tu vois ça sur la parabole représentative de la fonction carré)
-Quand x->-inf , -x->+inf (d'accord ? ça parait évident, non ?)
Donc quand x->-inf , -x-1->+inf (le -1 il est négligeable par rapport à +inf)
-Quand x->-inf , 1/x->0 (regarde la représentation de la fonction inverse, tu vois que quand x tend vers -inf, 1/x se "rapproche" de 0. D'accord ?)
Bon et bien maintenant il suffit d'additionner :
-inf + -inf + 0 -> -inf
Tu étais où quand vous avez fait le cours sur les limites ... ?
Tu l'as ?
Limites des fonctions usuelles :
-Quand x->-inf , x²->+inf (d'accord ? Tu vois ça sur la parabole représentative de la fonction carré)
-Quand x->-inf , -x->+inf (d'accord ? ça parait évident, non ?)
Donc quand x->-inf , -x-1->+inf (le -1 il est négligeable par rapport à +inf)
-Quand x->-inf , 1/x->0 (regarde la représentation de la fonction inverse, tu vois que quand x tend vers -inf, 1/x se "rapproche" de 0. D'accord ?)
Bon et bien maintenant il suffit d'additionner :
-inf + -inf + 0 -> -inf
Tu étais où quand vous avez fait le cours sur les limites ... ?
je ne comprend pas pourquoi elle est inutile en -inf
f(x)=x²-x-1+(1/x)
tu sais que tu peux ecrire que f(x)=x²+(-x)-1+1/x
dans ton cours tu as vu que:
de même tu sais que
de même
(en fait si on ecrivait vers quoi chaque terme tend ça donnerait
donc
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
