Bonjour a tous
Soit la fonction f(x) = ((1)/(4))x^(2)-1
1/ Etudier f et tracer et tracer sa courbe representative Cf dans un repere orthonormé
2/ deduire la courbe Cg de la fonction g définie sur ℝ par g(x) = |((1)/(4))x^(2)-1| et dresser son tableau de variation
3/ Determiner graphiquement et suivant les valeurs du paramétre reel m le nombre de solution de l'equation : | 4 − x² | =m.
je bloque a partir de la question 2 . Merci a votre aide
Les fonctions
3 messages
- Page 1 sur 1
Re: les fonctions
là où f(x) est positive, g(x)=f(x), g y a les mêmes variations que f
là où f(x) est négative g(x)=-f(x), g a des variations opposées à celles de f
là où f(x) est négative g(x)=-f(x), g a des variations opposées à celles de f
Re: les fonctions
Bonjour;
1.
 est une fonction polynomiale , donc son domaine de définition est :
est une fonction polynomiale , donc son domaine de définition est :  .
.
 on a :
on a :  ; et
; et  = \dfrac{1}{4}(-x)^2-1= \dfrac{1}{4}x^2-1 = f(x)) ;
;
donc est une fonction paire , donc on peut l'étudier sur
est une fonction paire , donc on peut l'étudier sur  .
.
On a : = \underset{x\rightarrow +\infty}{lim} \dfrac{1}{4}x^2-1 =+\infty) .
.
 = \dfrac{1}{2}x) , donc :
, donc : 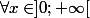 on a
on a >0) donc f est strictement croissante sur
donc f est strictement croissante sur  ;
;
de plus , pour on a
on a  = 0) ; donc
; donc  admet un extremum pour
admet un extremum pour 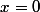 . Cet extremum est un minimum car le coefficient de second degré de la fonction polynomiale de second degré est
. Cet extremum est un minimum car le coefficient de second degré de la fonction polynomiale de second degré est =-1) .
.
Enfin ,=0) sur
sur  si
si ^2-1 = 0) ; donc si
; donc si 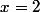 .
.

2.
D'après la courbe on déduit
on déduit 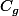 en suivant les indications de Pascal .
en suivant les indications de Pascal .
Le tableau de variation de g est automatiquement déduit de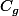 .
.

A toi maintenant de faire la suite .
1.
donc
On a :
de plus , pour
Enfin ,

2.
D'après la courbe
Le tableau de variation de g est automatiquement déduit de

A toi maintenant de faire la suite .
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 85 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
