Au niveau déstabilisation", ces vrai que les premières années à la fac sont un peu déstabilisé par ce qu'on leur demande (eh, m'sieur, à l'exam y'avais un exo qu'on avais même pas fait exactement le même avant...), et je peut te garantir qu'on leur demande BEAUCOUP moins théorique que ça.
En ce qui concerne la notion de classe d'équivalence, ben il semble que c'est plus trop la mode... (à mon époque, on en parlait dés la quatrième pour définir les quotients et les vecteurs...).
Faut reconnaitre que chez beaucoup d'étudiants, ça coince pas mal... et comme on peut arriver à manipuler à peu prés correctement les quotients, les vecteurs et les congruences sans parler de classes d'équivalences, et ben on les a de plus en plus repoussées dans les programmes.
En ce qui concerne
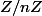
, au départ, on définit la notion
de congruence modulo n :
Soit n, a et b trois entiers relatifs. On dit que a et b sont congrus modulo n lorsque b-a est un multiple (entier) de n. On écrit
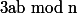
ou, plus simplement
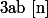
.
Il est clair que, pour n fixé, c'est une
relation d'équivalence :
Réflexive : pour tout entier a
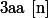
Symétrique : pour tout entiers a,b, si
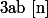
alors
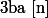
Transitive : pour tout entiers a,b,c, si
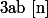
et
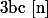
alors
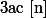
On peut donc parler des
classe d'équivalences modulo n: pour un entier a donné, la classe de a modulo n est l'ensemble des entier x tels que
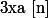
=\{x\in{\bb Z}\ {\rm t.q.}\ x\equ a\ [n]\})
s'il n'y a pas d'ambiguité sur la valeur de n, on utilise fréquement la notation
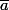
pour la classe de a.
Un exemple :
Si n=5, la classe de 3 est
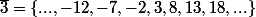
Le trés gros intérêt de la notion est de pouvoir remplacer une congruence, par exemple
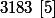
par une vrai égalité
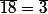
.
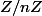
, est alors l'ensemble des classes d'équivalences modulo n.
Il est assez clair qu'en fait
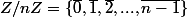
où, évidement, les barres désignent les classes modulo n.
Tient, pour voir si tu suit, qui est
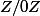
? et
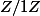
?
