Khôlle : Un brin de groupe dans Lagrange.
Bon, j'arrive (j'était en train de faire mon jardin...)
Je suppose que l'exo de nightmare, c'est ça le début :
Là, comme Nightmare le précise, il faut supposer en plus que G est de cardinal fini.
Ici, on regarde le cas de Z/nZ (avec ). Muni de la loi + c'est un groupe, mais ici, ce n'est pas la loi + qui nous interesse, mais la loi
). Muni de la loi + c'est un groupe, mais ici, ce n'est pas la loi + qui nous interesse, mais la loi  .
.
Muni de cette loi, Z/nZ n'est jamais un groupe car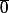 n'est jamais inversible (l'élément neutre pour la loi
n'est jamais inversible (l'élément neutre pour la loi  est
est 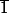 et
et  fois n'importe quoi ne fait jamais
fois n'importe quoi ne fait jamais 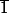 )
)
Donc la question de Nightmare est : "Quels sont les éléments de Z/nZ qui admettent des inverses pour la loi "
"
Ensuite, tu pourra montrer que l'ensemble de ces éléments forme un groupe (évidement toujours pour la loi ) et, si ça t'interesse, regarder comment calculer assez simplement le nombre d'éléments.
) et, si ça t'interesse, regarder comment calculer assez simplement le nombre d'éléments.
Tu en déduira alors le théorème dit d'Euler (c'est une généralisation du petit théorème de fermat)
Je suppose que l'exo de nightmare, c'est ça le début :
Là, le mieux, c'est vraiment de voir G comme un groupe absolument quelconque, (pas nécéssairement commutatif) dont la loi est notée multiplicativement.Nightmare a écrit:Quelque chose qui peut t'être utile : On considère l'ensembleavec g donné dans G . Tu peux montrer que cet ensemble est un sous-groupe de G dit monogène
Nightmare a écrit:L'idée principale est de voir que, vu que le groupe est fini, cet ensemble va "boucler" au sens ou l'on va forcément au bout d'un moment tomber sur un entier n tel que. Le plus petit entier vérifiant cette égalité est appelé l'ordre de g, qui est alors le cardinal du groupe . (Tout ce qui est dit ici, tu peux le montrer).
Par Lagrange qu'on vient de démontrer, on sait donc que l'ordre de g divise le cardinal de G.
Là, comme Nightmare le précise, il faut supposer en plus que G est de cardinal fini.
Nightmare a écrit:Maintenant question pour toi : Combien il y a dans Z/nZ d'éléments (= classes d'élément) inversibles, ie d'éléments m tels qu'il existe p tel que?
On approche de très près le théorème d'Euler...
Ici, on regarde le cas de Z/nZ (avec
Muni de cette loi, Z/nZ n'est jamais un groupe car
Donc la question de Nightmare est : "Quels sont les éléments de Z/nZ qui admettent des inverses pour la loi
Ensuite, tu pourra montrer que l'ensemble de ces éléments forme un groupe (évidement toujours pour la loi
Tu en déduira alors le théorème dit d'Euler (c'est une généralisation du petit théorème de fermat)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
"A la base", comme tu dit, le groupe est noté multiplicativement (sinon, g^n ça voudrait rien dire)
Comme exemple, je peut te donner :
Le complexe i du groupe) qui est d'ordre 4.
qui est d'ordre 4.
La permutation) du groupe des permutations de {1..5} (muni de la loi o) : elle est d'ordre 6.
du groupe des permutations de {1..5} (muni de la loi o) : elle est d'ordre 6.
L'élément du groupe (Z/18Z,+) qui est d'ordre 9.
du groupe (Z/18Z,+) qui est d'ordre 9.
P.S. :
1) ça veut pas dire grand chose un groupe "additif" : dans un groupe, il y a une loi et on peut la noter à priori comme on veut, mais c'est une notation, c'est tout. En plus, à peu prés tout le monde note '+' la loi d'un groupe uniquement lorsqu'il est commutatif (j'ai pas l'habitude que a+b soit différent de b+a, quelque soit le contexte...) Dans un groupe quelconque (i.e. qu'on connait pas) et pas nécéssairement commutatif, la loi est en général noté '.' ou ou... rien du tout.
ou... rien du tout.
2) Essaye de faire les questions dans l'ordre :
G un groupe absolument quelconque dont la loi sera noté multiplicativement.
Pour un g dans G et un n dans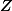 , on définit :
, on définit :
\ \ \ \ \ \ \ \ &{\rm si}\ n\geq1\ \ \cr<br />1_G\ ({\rm l'element neutre})\ \ \ &{\rm si}\ n=0\ \ \cr<br />g^{-1}.g^{-1}...g^{-1}\ (-n\ {\rm fois})\ &{\rm si}\ n\leq-1\cr<br />}\right.)
Est ce que tu vois pourquoi l'ensemble des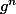 (pour g fixé) est un sous groupe de G ?
(pour g fixé) est un sous groupe de G ?
Comme exemple, je peut te donner :
Le complexe i du groupe
La permutation
L'élément
P.S. :
1) ça veut pas dire grand chose un groupe "additif" : dans un groupe, il y a une loi et on peut la noter à priori comme on veut, mais c'est une notation, c'est tout. En plus, à peu prés tout le monde note '+' la loi d'un groupe uniquement lorsqu'il est commutatif (j'ai pas l'habitude que a+b soit différent de b+a, quelque soit le contexte...) Dans un groupe quelconque (i.e. qu'on connait pas) et pas nécéssairement commutatif, la loi est en général noté '.' ou
2) Essaye de faire les questions dans l'ordre :
G un groupe absolument quelconque dont la loi sera noté multiplicativement.
Pour un g dans G et un n dans
Est ce que tu vois pourquoi l'ensemble des
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Je ne suis pas sur d'avoir compris le troisième exemple :doh: déjà que c'est pas mal abstrait pour moi Z/nZ même si ça représente les congruences modulo n.
donc là c'est mod 18 10={...;-8;10;28...}
et donc en fait ici par exemple si on prend 10 on a 10+10+10...=90=9*18
si j'ai bien compris ... ( ça doit être ça.)
En ce qui concerne le fait que les g^n forment un sous groupe et bien je suis très embêté. Faudrait montrer justement qu'il existe n tel que g^n=1 et que tout élément est inversible.
Pour le premier je dirais qu'il faut prendre n=0 et pour la deuxième condition qu'il faille prendre -n car en effet g^n * g^-n = g^0=1
ce qui devrait suffir a prouver que les g^n forment un sous groupe de G car de plus on vérifie facilement que les g^n appartiennent à G.
donc là c'est mod 18 10={...;-8;10;28...}
et donc en fait ici par exemple si on prend 10 on a 10+10+10...=90=9*18
si j'ai bien compris ... ( ça doit être ça.)
En ce qui concerne le fait que les g^n forment un sous groupe et bien je suis très embêté. Faudrait montrer justement qu'il existe n tel que g^n=1 et que tout élément est inversible.
Pour le premier je dirais qu'il faut prendre n=0 et pour la deuxième condition qu'il faille prendre -n car en effet g^n * g^-n = g^0=1
ce qui devrait suffir a prouver que les g^n forment un sous groupe de G car de plus on vérifie facilement que les g^n appartiennent à G.
Impecable.
Mes trois "exemples" était là pour bien te montrer qu'en fonction de la loi du groupe, le fait qu'un élément soit d'ordre n s'écrit de façon différente :
Le complexe i du groupe) est d'ordre 4 car
est d'ordre 4 car  qui est l'élément neutre du groupe (et, si on met moins de 4 fois
qui est l'élément neutre du groupe (et, si on met moins de 4 fois  , ça ne fait pas
, ça ne fait pas  )
)
La permutation) du groupe des permutations de {1..5} (muni de la loi o) est d'ordre 6 car
du groupe des permutations de {1..5} (muni de la loi o) est d'ordre 6 car  qui est l'élément neutre du groupe (et, si on met moins de 6 fois
qui est l'élément neutre du groupe (et, si on met moins de 6 fois  , ça ne fait pas
, ça ne fait pas  ).
).
L'élément du groupe (Z/18Z,+) est d'ordre 9 car
du groupe (Z/18Z,+) est d'ordre 9 car  qui est l'élément neutre du groupe (et, si on met moins de 9 fois
qui est l'élément neutre du groupe (et, si on met moins de 9 fois  , ça ne fait pas
, ça ne fait pas 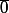 ).
).
Questions suivantes :
a) Si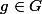 avec
avec  fini, montrer qu'il existe au moins un entier
fini, montrer qu'il existe au moins un entier  tel que
tel que  .
.
Le plus petit tel que
tel que  est appelé l'ordre de
est appelé l'ordre de  dans
dans 
b) Montrer que l'ordre de dans
dans 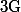 est en fait le cardinal du sous-groupe
est en fait le cardinal du sous-groupe  .
.
En déduire que l'ordre de divise le cardinal de
divise le cardinal de 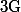
Remarque : Le cardinal (i.e. le nombre d'élément) d'un groupe fini est en général appellé l'ordre du groupe.
On vient donc de montrer que, dans un groupe fini, l'ordre de tout élément divise l'ordre du groupe.
Ensuite, tu regardera l'application de ce résultat aux éléments inversible (pour la loi ) de Z/nZ.
) de Z/nZ.
Mes trois "exemples" était là pour bien te montrer qu'en fonction de la loi du groupe, le fait qu'un élément soit d'ordre n s'écrit de façon différente :
Le complexe i du groupe
La permutation
L'élément
Questions suivantes :
a) Si
Le plus petit
b) Montrer que l'ordre de
En déduire que l'ordre de
Remarque : Le cardinal (i.e. le nombre d'élément) d'un groupe fini est en général appellé l'ordre du groupe.
On vient donc de montrer que, dans un groupe fini, l'ordre de tout élément divise l'ordre du groupe.
Ensuite, tu regardera l'application de ce résultat aux éléments inversible (pour la loi
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 84 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
