Khôlle : Un brin de groupe dans Lagrange.
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Avr 2010, 13:28
par Nightmare » 17 Avr 2010, 13:28
Pourquoi g^(n+1)=g ? Pourquoi les n autres sont distincts? C'est généralement faux (la deuxième affirmation en tout cas, g^n=1, c'est déjà plus vrai..)
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 17 Avr 2010, 13:37
par benekire2 » 17 Avr 2010, 13:37
Nightmare a écrit:Pourquoi g^(n+1)=g ? Pourquoi les n autres sont distincts? C'est généralement faux (la deuxième affirmation en tout cas, g^n=1, c'est déjà plus vrai..)
C'est où que j'ai merder ? La a- est juste au moins ??
g^(n+1)=gg^n or g^n=1 d'où g^(n+1)=g
et puis je vois pas pourquoi ils ne seraient pas distincts les g^n de 1 à n-1 ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Avr 2010, 13:40
par Nightmare » 17 Avr 2010, 13:40
Pourquoi g^n=1? C'est vrai mais pourquoi?
Pour l'autre affirmation, si je reprends par exemple le groupe des permutations de [|1,n|], je considère une transposition quelconque, elle est toujours d'ordre 2 et non n et par exemple, g^3=g.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 17 Avr 2010, 13:48
par benekire2 » 17 Avr 2010, 13:48
je crois qu'on s'est embrouillé dans les notations. J'ai pas utilisé pareil que toi.
G un groupe fini et H un sous groupe. Soit m l'ordre de H. On a par définition g^m=1 et donc g^(m+1)=g
Et tout les éléments du sous groupe engendré par g ( de 1 à m) sont distincts.
[ici m n'est pas le cardinal de G]
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 17 Avr 2010, 16:52
par benekire2 » 17 Avr 2010, 16:52
finalement c'est juste ce que j'ai écrit ou pas ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Avr 2010, 16:54
par Nightmare » 17 Avr 2010, 16:54
Qui est H? Qui est g? Si H= alors par définition on a ce que tu as écrit, si H est juste une sous-groupe d'ordre m et g un élément, alors g^m=1 est à montrer...
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 17 Avr 2010, 16:57
par benekire2 » 17 Avr 2010, 16:57
ba on l'a montré déjà, on a dit qu'il existait m tel que g^m=1 et que on appelait m l'ordre de g.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Avr 2010, 17:02
par Nightmare » 17 Avr 2010, 17:02
Tu as dit que m était l'ordre de H pas celui de g ! Comme Ben te l'a dit, si H=, ils correspondent, maintenant on a aussi le résultat que tu stipules, à savoir que si H est un groupe quelconque d'ordre m et g un élément de H, alors g^m=1. Maintenant la question : pourquoi?
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 17 Avr 2010, 17:22
par benekire2 » 17 Avr 2010, 17:22
bah, mettons que g est un élément de H. Posons H d'ordre m et g d'ordre n, on a : g^n=1 or par lagrange on sait que l'ordre de g divise l'ordre de H. Donc, m=kn d'où g^(kn)=1
Maintenant, la suite ... et ça c'est moins drôle :zen:
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 17 Avr 2010, 17:46
par benekire2 » 17 Avr 2010, 17:46
mp=1[n] <=> mp-kn=1
donc d'après bezout comme on travaille avec m et n libres , et qu'on veut trouver k et p on doit donc avoir PGCD(m,n)=1
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Avr 2010, 18:08
par Nightmare » 17 Avr 2010, 18:08
Ca me va pour les deux. Et pour un entier n fixé, combien il y a-t-il d'entier m inférieur qui lui sont premiers?
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 17 Avr 2010, 18:36
par benekire2 » 17 Avr 2010, 18:36
Bah je dirais qu'on peut pas savoir directement, mais après une rapide recherche, il existe une fonction qui nous fait ça qui s'appelle l'indicatrice d'Euler
Est-ce ça ? Ou alors il y a un autre moyen ??
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Avr 2010, 18:43
par Nightmare » 17 Avr 2010, 18:43
Sans parler de l'indicatrice d'Euler pour le moment, tu devrais pouvoir les compter en prenant pas à pas des cas particulier. Le cas n=p premier est simple, tu peux traiter ensuite le cas n=p^k avec p premier et ensuite essayer de trouver l'expression pour n quelconque en utilisant la décomposition en facteur premier.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 17 Avr 2010, 18:49
par benekire2 » 17 Avr 2010, 18:49
avec n=p on en a p-1
Après je réfléchis ..
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 17 Avr 2010, 19:38
par benekire2 » 17 Avr 2010, 19:38
pour p^k on trouve (p-1)*p^(k-1) nombres premiers avec p^k

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 17 Avr 2010, 19:48
par Ben314 » 17 Avr 2010, 19:48
Jusque là, c'est O.K.
En fait le cas d'un nombre premier p prouve déja le petit théorème de fermat :
"Si n est premier avec p alors

"
Sinon, perso, avant de compter le nombre d'inversibles de Z/nZ, j'aurais bien rajouté comme question :
Est il clair que les éléments inversibles de Z/nZ forment un groupe (évidement pour la loi

) ?
P.S. Pour compter le nombre d'éléments inversibles dans Z/nZ avec n quelconque, je sais pas s'il y a un moyen simple sans utiliser ce que l'on apelle "le théorème chinois"...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 17 Avr 2010, 19:52
par benekire2 » 17 Avr 2010, 19:52
finalement je tombe sur
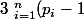p_i^{k_i-1})
Avec
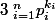
la décomposition en produit de facteur premiers de notre nombre.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 17 Avr 2010, 20:04
par Ben314 » 17 Avr 2010, 20:04
C'est bien ça,
mais tu as fait comment pour le trouver ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 17 Avr 2010, 20:07
par benekire2 » 17 Avr 2010, 20:07
Ben314 a écrit:Jusque là, c'est O.K.
En fait le cas d'un nombre premier p prouve déja le petit théorème de fermat :
"Si n est premier avec p alors

"
Sinon, perso, avant de compter le nombre d'inversibles de Z/nZ, j'aurais bien rajouté comme question :
Est il clair que les éléments inversibles de Z/nZ forment un groupe (évidement pour la loi

) ?
P.S. Pour compter le nombre d'éléments inversibles dans Z/nZ avec n quelconque, je sais pas s'il y a un moyen simple sans utiliser ce que l'on apelle "le théorème chinois"...
Euh ... comment on le prouve le petit théorème de fermat avec ce que j'avais écrit ? Je vois pas trop en fait ...
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 17 Avr 2010, 20:12
par benekire2 » 17 Avr 2010, 20:12
Ben314 a écrit:C'est bien ça,
mais tu as fait comment pour le trouver ?
Ben c'est une conjecture .... je l'ai pas réellement prouvé

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 78 invités
 "
" ) ?
) ?"
) ?
