Justifier: f(x) a une solution unique (An)

[Anonyme]

Bonjour,
Je suis bloqué sur une question de mon DM.


Enoncé:
Pout tout n supérieur ou égal a 1, on considère la fonction Fn définie sur [0;+inf[ par:
Fn(x)=ln(x)-2+x^2/n

1.a.Etudier les variations de Fn et étudier ses limites en 0 et +inf

J'ai trouver comme dérivée:
F'n(x)=n[n^2+x^2(2n-X)]/xn^3
Mais je ne sais pas si elle est juste

Et les limites:
En 0: -inf
En +inf: +inf

1.b.Justifier que l'équation Fn(x)=0 a une solution unique notée (alpha)n.

Et la je bloque !

[Zebulon]

Bonjour,
la dérivée n'est pas bonne: je trouve
sur
donc est croissante sur .
Les limites sont bonnes.
Et là tu dois utiliser LE théorème importantissime en analyse (en terminale), en montrant que ses hypothèses sont vérifiées, pour montrer que l'équation a une unique solution .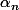
Bon courage et à bientôt,
Zeb.

[Quidam]

Fn(x)=ln(x)-2+x^2/n

D'abord il faudrait préciser :
S'agit-il de

ou de:

????

[Frangine]

Ou tout autre expression possible ...

il manque quelques parenthèses pour préciser le sujet !!!!

[leditvalentin]

Fn(x)=ln(x)-2+[(x^2)/(n)]
Excusez moi.

Pour la dérivée j'ai d'abord décomposé (x^2)*(1/n)
Et ensuite j'ai dérivée avec la formule u'v+uv'.

[Zebulon]

Bonjour,
Attention! Tu dérives par rapport à x! Il n'y a pas de dérivées par rapport à n.
Zeb.