Jouer avec les entiers (1S)

[Anonyme]

Bonjour,
Voila un ptit exercice ds le manuel de 1ere S:
Demontrer que la somme de 4 entiers naturels consecutifs augmenté de 1 est le carre d'un entier naturel

Comment faire?
a+

[allomomo]

Salut,

interprétation :
x et n des entiers naturels


Mais je ne sais pas si c'est vrai

[becirj]

C'est faux : (2+3+4+5)+1 n'est pas le carré d'un naturel.

[allomomo]

oui j'ai essayer avec plusieurs mais cela ne marche pas

[Anonyme]

youps, je me suis trompée, dsl
c le produit de 4 entiers naturels augmente de 1 qui est egale a un carre

[becirj]

On développe le produit x(x+1)(x+2)(x+3)+1.
On obtient un polynôme de degré 4. Si c'est un carré, c'est le carré d'un polynôme du second degré de la forme , on calcule le carré d'un tel polynôme et on cherche s'il est possible de trouver a, b et c pour que les 2 polynômes soient égaux.

[Anonyme]

Bonsoir
Merci mais je n'y arrive pas....
en mettant au carre le polynome P(x)de 2nd degre, je trouve:
a^2x^2+2abx^3+x^2(2ac+b^2)+2bc+c^2
et cela ne va pas, car, a devrai etre eagl a a (puisque il y a 1*n^4), et c devrait aussi etre egal a 1 (car ds l autre polynome, il y a +1)
Donc, rien ne va....
Si vous pouvez m aider, merci d'avance

[becirj]

Il y a des erreurs (de frappe ?) dans le développement du carré : on obtient:
Le produit des 4 entiers consécutifs plus 1 est égal à :
On doit donc avoir :





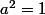
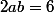
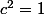
On démarre avec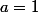 ou 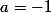(puisque l'on veut un naturel on conserve 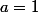, on déduit les valeurs de b et c en prenant deux autres équations et on vérifie que les deux dernières sont vérifiées.

[Anonyme]

Merci beaucoup
(oui, c'etait une erreur de frappe)
Mon porbleme, c'est que j ai recopie sur ma feuille: ab=6 au lieu de 2ab=6, c'est pour ca que je n'arrivait pas a trouver
Les resultats sont: a=1; b=3; c=1
Merci encore