Iteration et suite
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 23 Juil 2012, 09:15
par fatal_error » 23 Juil 2012, 09:15
salut à tous,
un petit exo custom (plus un problème sur lequel je penche et sur lequel je vais bientot me pendre, accessible aux lycéens)
On a une une valeur initiale 0Mettons k = 1/10.
A chaque iteration, on a
Iter(n) = Iter(n-1) * a(n)
avec Iter(0)=k
Le but est de trouver une suite a(n), telle que pour i=1 à n=m (m étant un paramètre supérieur 1)
0Iter(n+1)-Iter(n)Iter(m) = 1
A votre imagination
la vie est une fête

-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 23 Juil 2012, 11:51
par Cliffe » 23 Juil 2012, 11:51
Yop,
[CENTER]

[/CENTER]
mais sa ne respecte pas l'inégalité :we:
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 23 Juil 2012, 12:15
par Skullkid » 23 Juil 2012, 12:15
Salut,
a+k}{(2^{n-1}-1)a+k})
avec

doit marcher, aux erreurs de calcul près.

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 23 Juil 2012, 12:42
par fatal_error » 23 Juil 2012, 12:42
pour ma part,
avec n termes. a_n=u_n
(1)

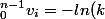)
avec
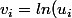)
}{n})
est solution triviale de (1).
L'idée est de construire
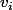
décroissante.
par exemple on prend

, et

, de facon à préserver la somme sur
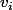
.
Posons
}{n})

on peut construire la droite

avec
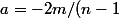)
et
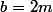
Et on déduit
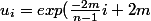 = exp(2m (1 - \frac{i}{n-1})))
reste à vérifier les condo, mais ca va.
la vie est une fête


-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 23 Juil 2012, 12:43
par fatal_error » 23 Juil 2012, 12:43
comment parviens-tu à
a+k}{(2^{n-1}-1)a+k})
?
la vie est une fête

-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 23 Juil 2012, 12:49
par Skullkid » 23 Juil 2012, 12:49
En fait je suis parti des inégalités. Mon idée c'était d'avoir
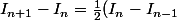)
, ce qui est possible avec
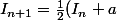)
avec a supérieur à 1. Reste à calculer le a pour qu'on tombe sur 1 en m étapes, puis à calculer le quotient des termes successifs de I.

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 23 Juil 2012, 13:26
par fatal_error » 23 Juil 2012, 13:26
ah, nice :id:
la vie est une fête

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités

 [/CENTER]
[/CENTER]